Дана трапеция ABCD, с основанием AD и BC. Постройте вектор а =вектор AB + вектор CD- вектор ВС. Найдите модуль вектора а, если АD = 12см, BC=5см.
Ответы на вопрос
Ответил ivanproh1
6
Ответ:
|а| = 2 см.
Объяснение:
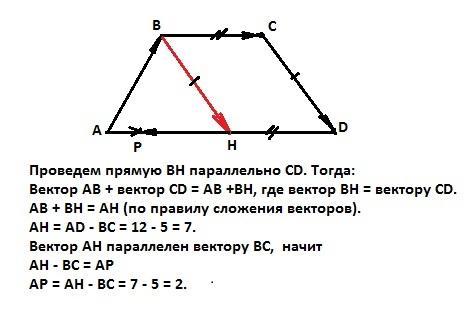
Проведем прямую ВН параллельно СD. Тогда:
Вектор АВ + вектор СD = AB +BH, где вектор ВН = вектору CD.
АВ + ВН = АН (по правилу сложения векторов).
АН = AD - HD (так как НD = BC как противоположные стороны параллелограмма) => AH = 12 - 5 = 7.
Или по теореме косинусов модуль суммы векторов равен:
|AH| = √(AD²-BC²-2·AD·BC·Cos0) = √(25+144-120) = 7.
Вектор AH параллелен вектору ВС, значит
АН - ВС = АР
АР = АН - ВС = 7 - 5 = 2.
Приложения:
Новые вопросы
Биология,
1 год назад
Химия,
1 год назад
Русский язык,
1 год назад
Английский язык,
1 год назад
Математика,
6 лет назад