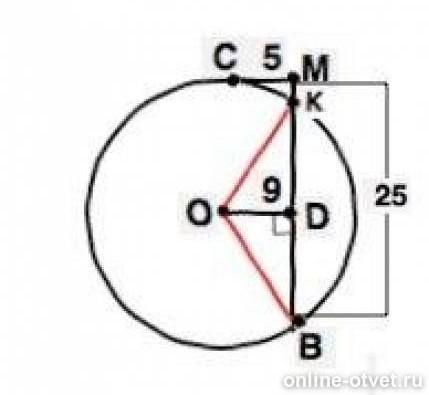
Дана окружность (О;ОС). Из точки М, которая находится вне окружности, проведена секущая МВ и касательная МС. OD-перпендикуляр, проведённый из центра окружности к секущей МВ и равный 6 см. Найди радиус окружности, если известно, что МВ равен 25 см и МС равен 15 см.

Ответ:

Обозначим вторую точку пересечения секущей с окружностью – К.

Если из одной точки проведены к окружности касательная и секущая, то произведение всей секущей на её внешнюю часть равно квадрату касательной.

СМ²=МВ•MK

25=25•MK ⇒ МК=1

ВК=25-1=24 см

ОК=ОВ – радиусы к точкам пересечения секущей и окружности.

∆ КОВ - равнобедренный, OD⊥KB ⇒OD - медиана и высота.

КD=24:2=12

Из ∆ OKD по т.Пифагора

OK²=KD²+OD² ⇒OK=√(144+81)

OK=R=√225= 15 см

Как я поняла , вот)

Как я поняла , вот)Можно лайк♡︎♡︎