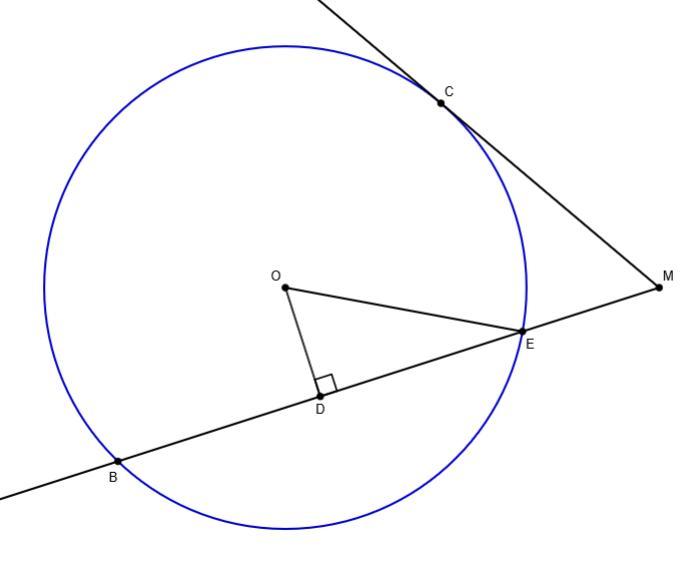
Дана окружность (O;OC). Из точки M, которая находится вне окружности, проведена секущая MB и касательная MC.
OD — перпендикуляр, проведённый из центра окружности к секущей MB и равный 6 см.
Найди радиус окружности, если известно, что MB равен 25 см и MC равен 15 см.

Теорема:  Если из одной точки к окружности проведены секущая и касательная, то произведение всей секущей на ее внешнюю часть равно квадрату отрезка касательной.

СМ² = МЕ * МВ    ⇒    МЕ = СМ²/МВ = 15²/25 = 225/25 = 9 см

ВЕ = МВ - МЕ = 25 - 9 = 16 см

Теорема:  Перпендикуляр, опущенный на хорду окружности, делит ее пополам.

BD = DE = BE/2 = 16/2 = 8 см

По теореме Пифагора:  

Ответ: 10 см.