Дана функция f(x)=x корень x+ 2 корень 2 / корень х + корень 2
а) покажите что f(x) = x + (ax)^1/2 + b, где а, b постоянные
б) найдите f'(x)
Приложения:
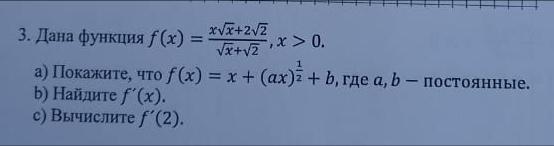
Ответы на вопрос
Ответил lilyatomach
1
Ответ:
а) a= 2, b = 2;
b)
c) f' (2) =0,5.
Объяснение:
Дана функция
а) Показать, что
где a, b - постоянные ( исправленное условие).
Воспользуемся формулой сокращенного умножения
a³ +b³ = ( a+b)(a²-ab+b²)
Тогда a= 2, b = 2.
b) Найти f' (x)
c) Вычислить
#SPJ1
Новые вопросы
Физика,
5 месяцев назад
Математика,
5 месяцев назад
История,
9 месяцев назад
Английский язык,
9 месяцев назад
Русский язык,
6 лет назад