Алгебра, вопрос задал pashakorben , 1 год назад

дана функция f(x)=x^3+6x^2+7x-2 напишите уравнение касательной к графику функции y=f(x) параллельной прямой y=-2x+7

Ответы на вопрос

Ответил Аноним

Производная данной функции $f'(x)=3x^2+12x+7$

Пусть $x_0$ - абсцисса точки касания прямой к кривой.

Известно, что неизвестная прямая(касательная) параллельна прямой y = -2x + 7, следовательно, у них угловые коэффициенты равны: k = -2.

По геометрическому смыслу производной, мы имеем:

$f'(x_0)=k\\ \\ 3x_0^2+12x_0+7=-2\\ \\ 3x_0^2+12x_0+9=0~~|:3\\ \\ x_0^2+4x_0+3=0$

По теореме Виета получаем $x_0=-3$ и $x_0=-1$

Т.е. имеет две касательные к данной кривой. Найдем их.

Общий вид уравнения касательной: $y=f'(x_0)(x-x_0)+f(x_0)$

Подсчитаем значение функции и значение производной функции в точке $x_0=-3$

$f(-3)=(-3)^3+6\cdot(-3)^2+7\cdot (-3)-2=4\\f'(-3)=3\cdot (-3)^2+12\cdot (-3)+7=-2$

Уравнение касательной: $y=-2(x+3)+4=\boxed{-2x-2}$

Аналогично, подсчитаем значение функции и значение производной функции в точке $x_0=-1$

$f(-1)=(-1)^3+6\cdot(-1)^2+7\cdot(-1)-2=-4$

$f'(-1)=3\cdot (-1)^2+12\cdot(-1)+7=-2$

Уравнение касательной: $y=-2(x+1)-4=\boxed{-2x-6}$

P.S. Можно было не считать значения производной функции, поскольку это и есть угловой коэффициент k = -2.

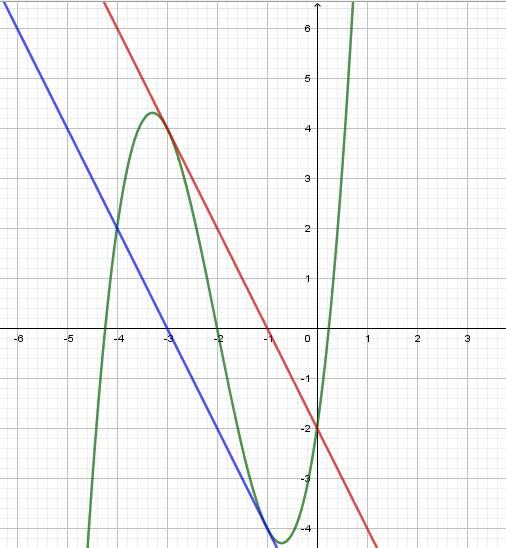
Приложения:

Новые вопросы

Русский язык, 1 год назад

Биология, 1 год назад

Математика, 1 год назад

Биология, 1 год назад

Алгебра, 6 лет назад

Қазақ тiлi, 6 лет назад