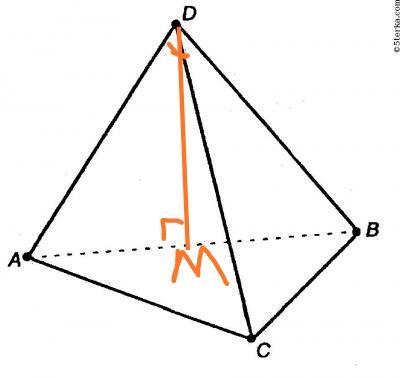
Дана Dabc-правильный тетраед,биссектриса DM-боковая грань равно 12.
Найти:АС+BD​​​​

Ответ: если я правильно поняла условие, то ДМ - это биссектриса боковой грани тетраэдра. В этом случае решение следующее:

АС+ВД=16√3

Объяснение:

Так как тетраэдр правильный, то все его грани являются правильными треугольниками и все его рёбра равны. Проведём биссектрису грани АДВ. Рассмотрим грань АДВ. Её биссектриса ДМ также является медианой и высотой, поэтому она делит эту грань на 2 равных прямоугольных треугольника АДМ и ВДМ, в которых сторона основания АВ и высота грани -ДМ катеты, а наклонные АД и ВД - гипотенуза. Поскольку АВД - правильный треугольник, то угол А=углуД=углуВ=60°. Найдём сторону АД через синус угла.

Синус угла - это отношение противолежащего от угла катета к гипотенузе поэтому:

АД=ДМ/sinA =12/sin60°=12÷√3/2=12×2/√3=

=24/√3. Избавимся от знака корня в знаменателе: (8×√3×√3)/√3=8√3

Итак: мы нашли одно ребро и так как они равны, так как тетраэдр правильный, то

АС=ВД=АД=8√3;

АС=ВД=АД=8√3;АС+ВД=8√3+8√3=16√3