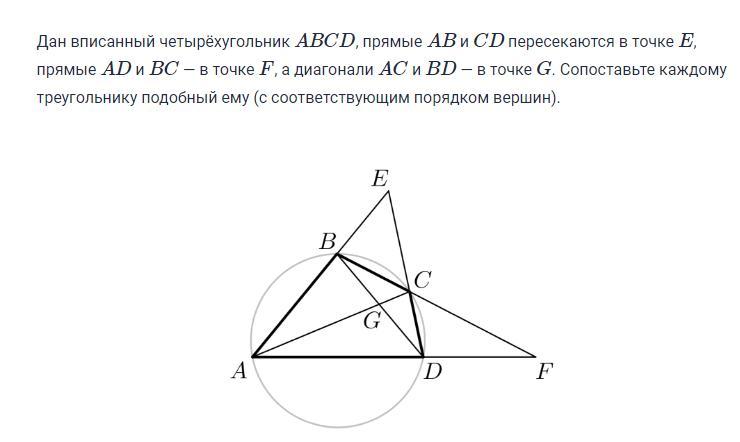
Дан вписанный четырёхугольник ABCD, прямые AB и CD пересекаются в точке E, прямые AD и BC — в точке F, а диагонали AC и BD — в точке G. Сопоставьте каждому треугольнику подобный ему (с соответствующим порядком вершин).



ACE
ABG
CDF
BCG
ACF
DAE
ADG
DBE
DCG
BDF
ABF
BCE

Дан вписанный четырёхугольник ABCD, прямые AB и CD пересекаются в точке E, прямые AD и BC — в точке F, а диагонали AC и BD — в точке G. Сопоставьте каждому треугольнику подобный ему (с соответствующим порядком вершин).

Объяснение:

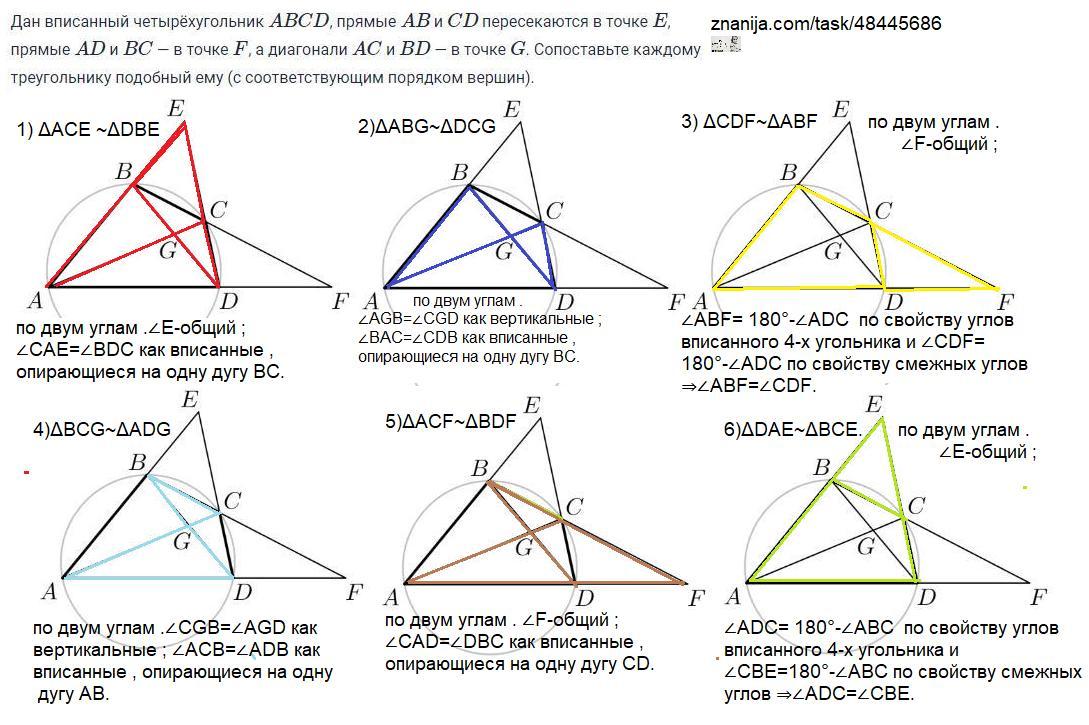
1) ΔACE ~ΔDBE по двум углам .∠Е-общий ; ∠САЕ=∠BDC как вписанные , опирающиеся на одну дугу ВС.

2)ΔABG~ΔDCG по двум углам .∠АGB=∠CGD как вертикальные ; ∠ВАС=∠СDB как вписанные , опирающиеся на одну дугу ВС.

3) ΔCDF~ΔABF по двум углам .∠F-общий ;

∠АВF= 180°-∠ADC  по свойству углов вписанного 4-х угольника и ∠СDF=180°-∠ADC по свойству смежных углов ⇒∠АВF=∠СDF.

4)ΔBCG~ΔADG по двум углам .∠СGB=∠АGD как вертикальные ; ∠АСВ=∠АDB как вписанные , опирающиеся на одну дугу АВ.

5)ΔACF~ΔBDF  по двум углам .∠F-общий ; ∠САD=∠DBC как вписанные , опирающиеся на одну дугу СD.

6)ΔDAE~ΔBCE.  по двум углам .∠E-общий ;

∠АDC= 180°-∠ABC  по свойству углов вписанного 4-х угольника и ∠СBE=180°-∠ABC по свойству смежных углов ⇒∠АDC=∠СBE.