Математика, вопрос задал lizalovelol606 , 6 лет назад

дан усеченный шар с радиусом 20 см расстояние от центра до плоскости составляет 12 см найти площадь сечения

Ответы на вопрос

Ответил mathkot

Ответ:

Площадь сечения 804,24 сантиметров квадратных

Пошаговое объяснение:

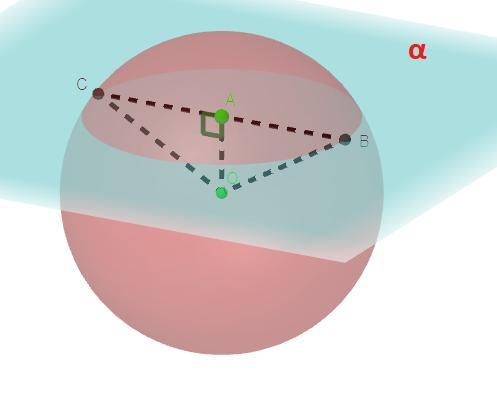
Дано: R = 20 см (R - радиус шара), OA ⊥ α, OA = 12 см, O - центр шара,

A - центр окружности в плоскости α

Найти: S - ?

Решение: Сечением шара плоскостью по определению является окружность .Проведем прямую которая пусть пересекает окружность с центром A в точках B и C, тогда отрезок BC по определению диаметр окружности с центром A. Так как по условию OA ⊥ α, то прямая OA перпендикулярна к любой прямой лежащей в плоскости α по следствию из определения перпендикулярности прямой к плоскости, то есть OA ⊥ BC. Так как точки B и C принадлежат шару, то отрезки OB и OC - радиусы шара. Так как точка A центр окружности, то она по свойству центра окружности делит диаметр пополам на два равных радиуса, то есть AC = AB = BC : 2. Рассмотрим прямоугольный(OA ⊥ BC) треугольник ΔAOC. По теореме Пифагора: $AC = \sqrt{OC^{2} - OA^{2} } = \sqrt{20^{2}-12^{2} } = \sqrt{400 - 144} = \sqrt{256} = 16$ см.