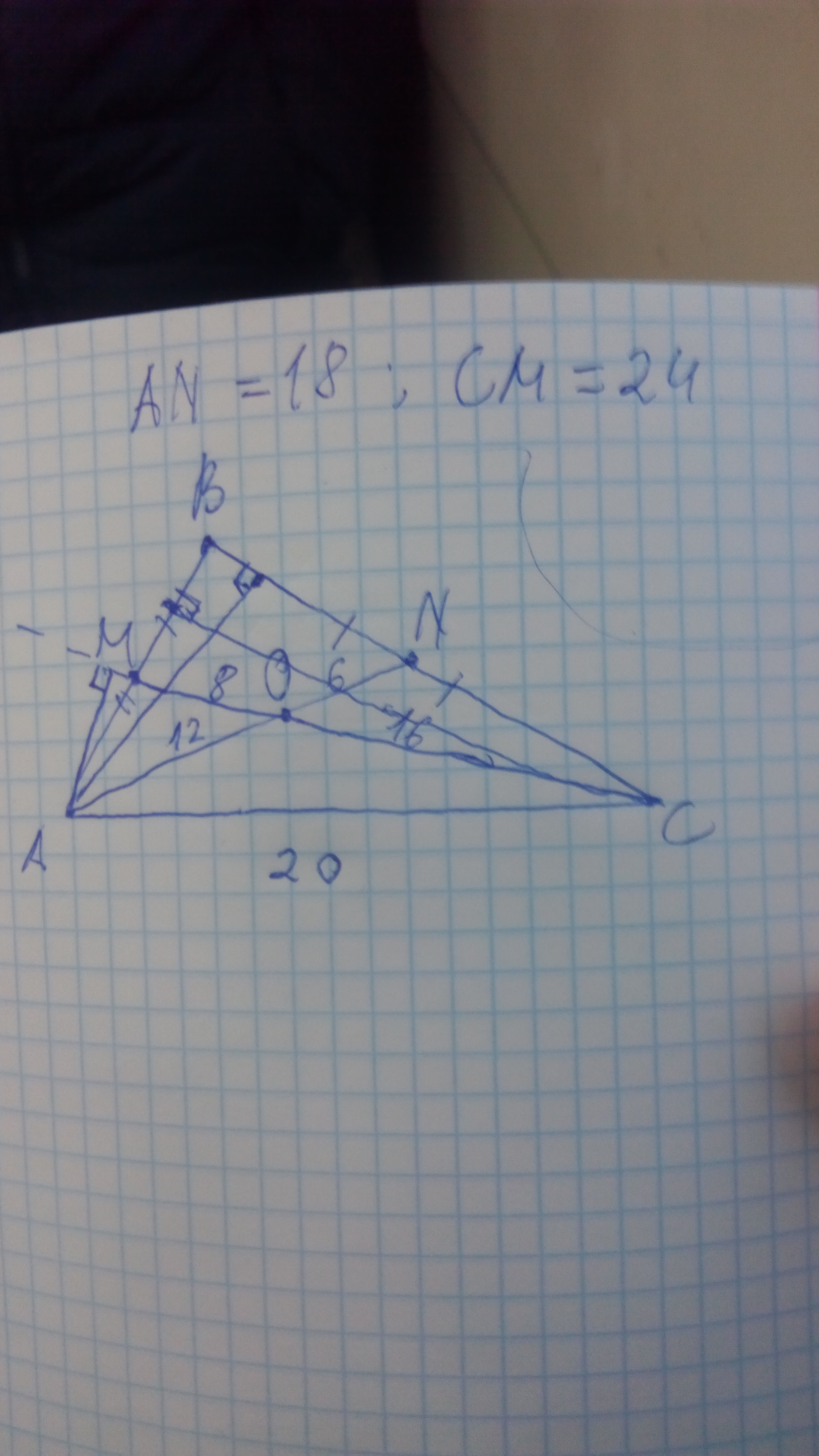
Дан треугольник, у которого длина основания 20см, а длины медиан,
проведенные к боковым сторонам равны 18 и 24 см. Чему равна площадь
данного треугольника?
Ответы на вопрос
Ответил mathgenius
0
Вспомним свойство что медианы точкой пересечения делиться как 2:1 считая от вершины,то есть:
AO/ON=2 ; CO/OM=2
Откуда: AO=2*18/3=12
CO=2*24/3=16.
Заметим, что треугольник AOC подобен египетскому прямоугольному треугольнику со сторонами 3,4,5 с коэффициентом подобия 4.
Значит его площадь: S(AOC)=12*16/2=96.
Тк треугольники AOC и AMC имеют общую высоту,то их площади относятся как основания,то есть:
S(AMC)/S(AOC)=MC/OC=3/2
S(AMC)=3/2 *S(AOC).
Треугольники ABC и AMC тоже имеют одну высоту,поэтому:
S(ABC)/S(AMC)=AB/AM=2
S(ABC)=2*S(AMC)=3*S(AOC)=3*96=
=288 см^2.
Вообще говоря известный факт ,что три медианы делят площадь треугольника на 3. Тк точка пересечения медиан его центр тяжести.
Приложения:
Новые вопросы
Английский язык,
2 года назад
Математика,
8 лет назад
Математика,
8 лет назад
Математика,
9 лет назад