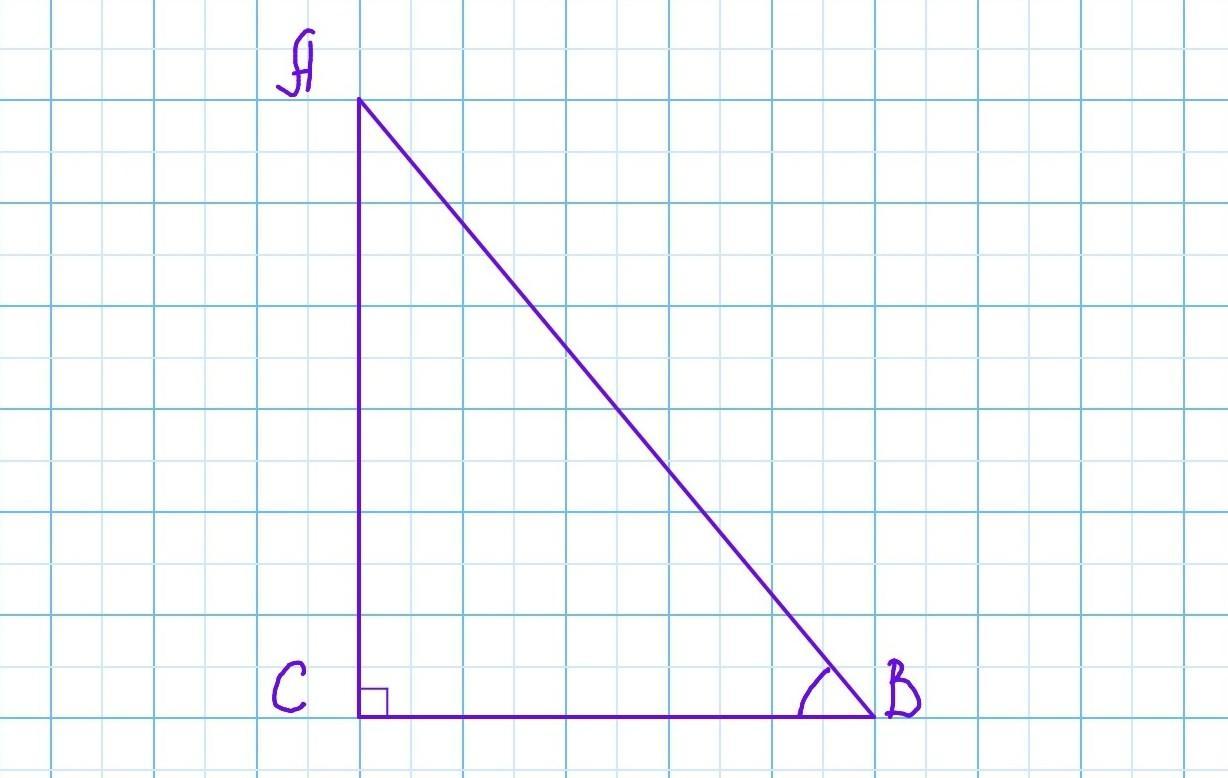
Геометрия, вопрос задал withoutfuture1337 , 2 года назад

Дан треугольник ABC, в котором ∠C=90°, а sinB=2√5/10√5, Найди cos2B.

Ответы на вопрос

Ответил ReMiDa

Дан треугольник ABC, в котором ∠C=90°, а

$sinB = \frac{2 \sqrt{5} }{ 10 \sqrt{5} }$

Найди cos²B.

Ответ:

cos²B=0,96

Объяснение:

Для начала упростим выражение:

$sinB = \dfrac{2 \sqrt{5} }{10 \sqrt{5} } = \dfrac{2}{10} = \dfrac{1}{5}$

Воспользуемся основным тригонометрическим тождеством:

Найдём cos²B:

${cos}^{2} B = 1 - {sin}^{2} B = 1 - { (\frac{1}{5}) }^{2} = \\ \\ = 1 - \dfrac{1}{25} = \dfrac{25 - 1}{25} = \frac{24}{25} = 0,96$

Приложения:

Новые вопросы

Английский язык, 1 год назад

Русский язык, 1 год назад

История, 2 года назад

Английский язык, 2 года назад

Алгебра, 8 лет назад

Математика, 8 лет назад