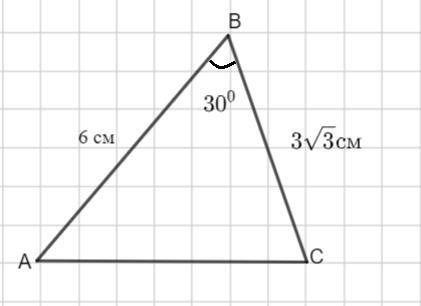
Геометрия, вопрос задал nasibaturdieva05 , 2 года назад

Дан треугольник ABC. Если AB = 6 см, BC =3 корень из 3

см и ∠B = 30°, то найди длину стороны AC.

Ответы на вопрос

Ответил lilyatomach

Ответ:

АС= 3 см.

Объяснение:

Рассмотрим треугольник АВС .

АВ=6 см, ВС=3√3 см, ∠В=30°.

По теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

$AC^{2}=AB^{2} +BC^{2} -2\cdot AB\cdot BC\cdot cos B;\\AC^{2}=6^{2} +(3\sqrt{3} )^{2} -2\cdot 6\cdot 3\sqrt{3} \cdot cos 30^{0} ;\\AC^{2} =36+27-2\cdot 18\sqrt{3} \cdot \dfrac{\sqrt{3} }{2} =36+27-18\cdot3=63-54=9\\$

$AC=\sqrt{9} =3$ см.

Приложения:

Ответил mathkot

Ответ:

AC = 3 см

Объяснение:

Дано: AB = 6 см, $BC = 3\sqrt{3}$ см, ∠B = 30°

Найти: AC - ?

Решение: По теореме косинусов:

$AC = \sqrt{AB^{2} + BC^{2} - 2AB * BC * \cos\angle B} = \sqrt{6^{2} + (3\sqrt{3} )^{2} - 2 * 6 * 3\sqrt{3} * \cos(30^{\circ})} =$ $\sqrt{36 + 27 - 2 * 6 * 3\sqrt{3} * 0,5\sqrt{3} } = \sqrt{63 - 64} = \sqrt{9} = 3$ см.