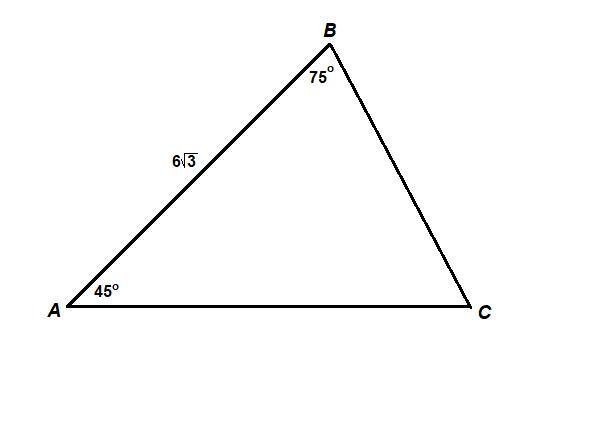
Дан треугольник ABC. Если AB = 6 корень из 3 см, ∠B = 75° и ∠A = 45°, то найди длину радиуса окружности, описанной около данного треугольника.

Ответ:

6 см

Объяснение:

Сумма углов треугольника равна 180°, тогда

∠С = 180° - (∠А + ∠В) = 180° - (45° + 75°) = 180° - 120° = 60°

По следствию из теоремы синусов, отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу описанной окружности:

 см