Дан шар диаметром 30 см. Стороны квадрата ABCD касаются поверхности шара. Расстояние от центра шара до плоскости квадрата равно 9 см. Найдите площадь квадрата. Рисунок обязателен.

Ответ:

Площадь квадрата равна 576 см².

Объяснение:

По условию дан шар диаметра 30 см.

Тогда радиус шара равен 15 см.

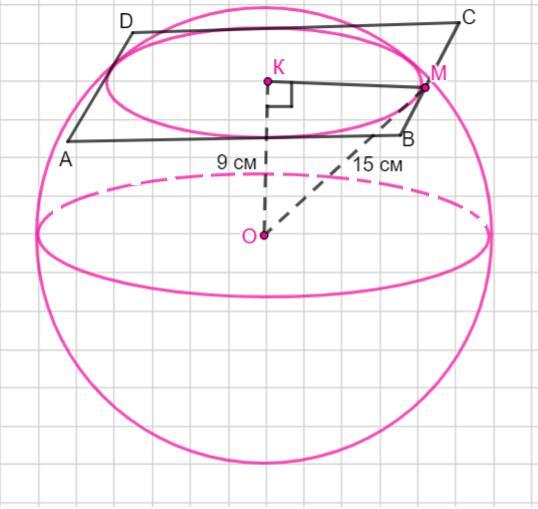
Стороны квадрата АВСD касаются поверхности шара. Построим сечение шара - окружность, вписанная в квадрат  с центром в точке К.

Центр шара - это точка  О. Если расстояние от центра шара до плоскости квадрата, то ОК = 9 см.

Точка М - точка касания стороны ВС  квадрата АВСD с поверхностью шара.

Тогда длина отрезка ОМ равна радиусу шара. ОМ = 15 см.

Рассмотрим Δ ОКМ - прямоугольный и найдем  катет КМ по теореме Пифагора: в прямоугольнм треугольнике квадрат гипотенузы равен сумме квадратов катетов.

cм.

Если КМ= 12 см, то сторона квадрата АВ= 24 см.

Найдем площадь квадрата по формуле

где а - сторона квадрата.

cм².