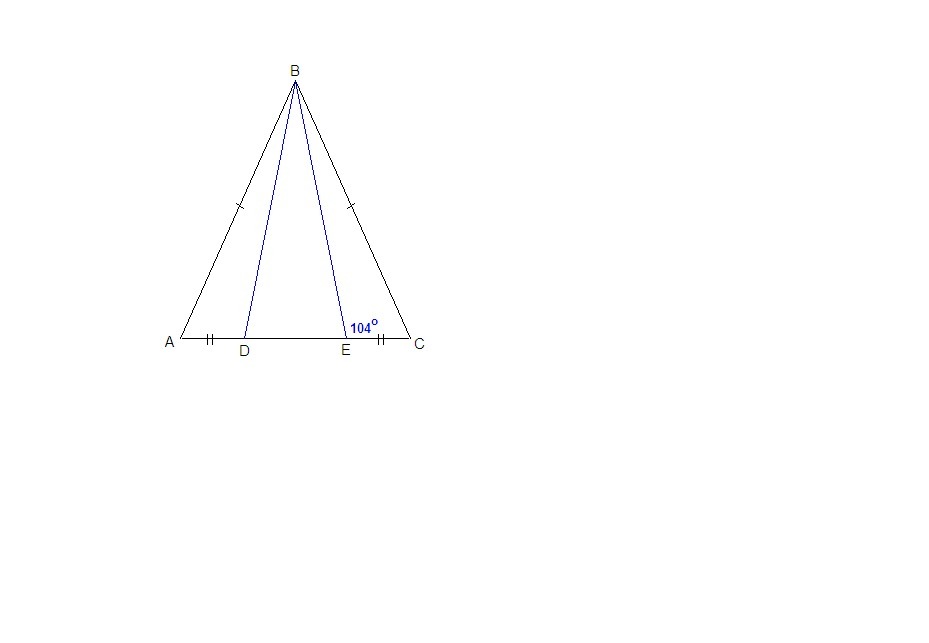
Дан равнобедренный треугольник ABC с боковыми сторонами AB=BC. На основании расположены точки D иE так, что AD=EC, ∡CEB=104°. Определи∡EDB.
Ответы на вопрос
Ответил KuOV
0
АВ = ВС, так как ΔАВС равнобедренный,
AD = CE по условию,
∠ВАС = ∠ВСА как углы при основании равнобедренного треугольника,
значит ΔВАD = ΔВСЕ по двум сторонам и углу между ними.
Следовательно BD = BE, т.е. ΔDBE равнобедренный, тогда
∠EDB = ∠BED как углы при основании равнобедренного треугольника.
∠EDB = 180° - ∠BEC = 180° - 104° = 76°
∠EDB = 76°
Приложения:
Новые вопросы
Химия,
2 года назад
Математика,
8 лет назад
Математика,
8 лет назад
Математика,
9 лет назад
История,
9 лет назад