Дан остроугольный треугольник ABC с углом 
Доказать, что вершины A и C треугольника, центр описанной окружности O, центр вписанной окружности I и ортоцентр H (то есть точка пересечения высот) лежат на одной окружности, и радиус этой окружности равен радиусу описанной окружности. Картинка желательна.
Ответы на вопрос
Ответил nabludatel00
0
Решение смотри последовательно в файлах.
Приложения:
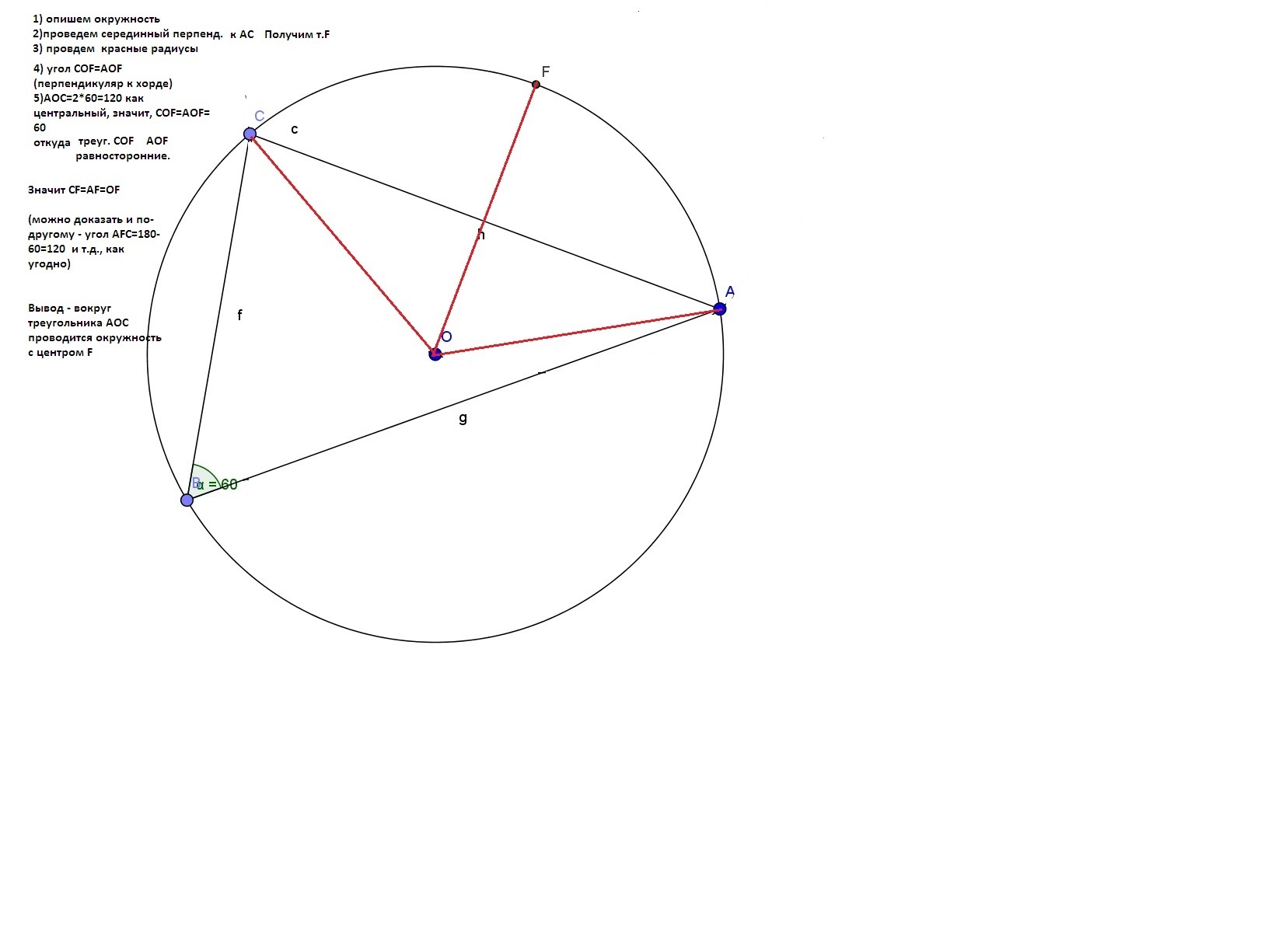
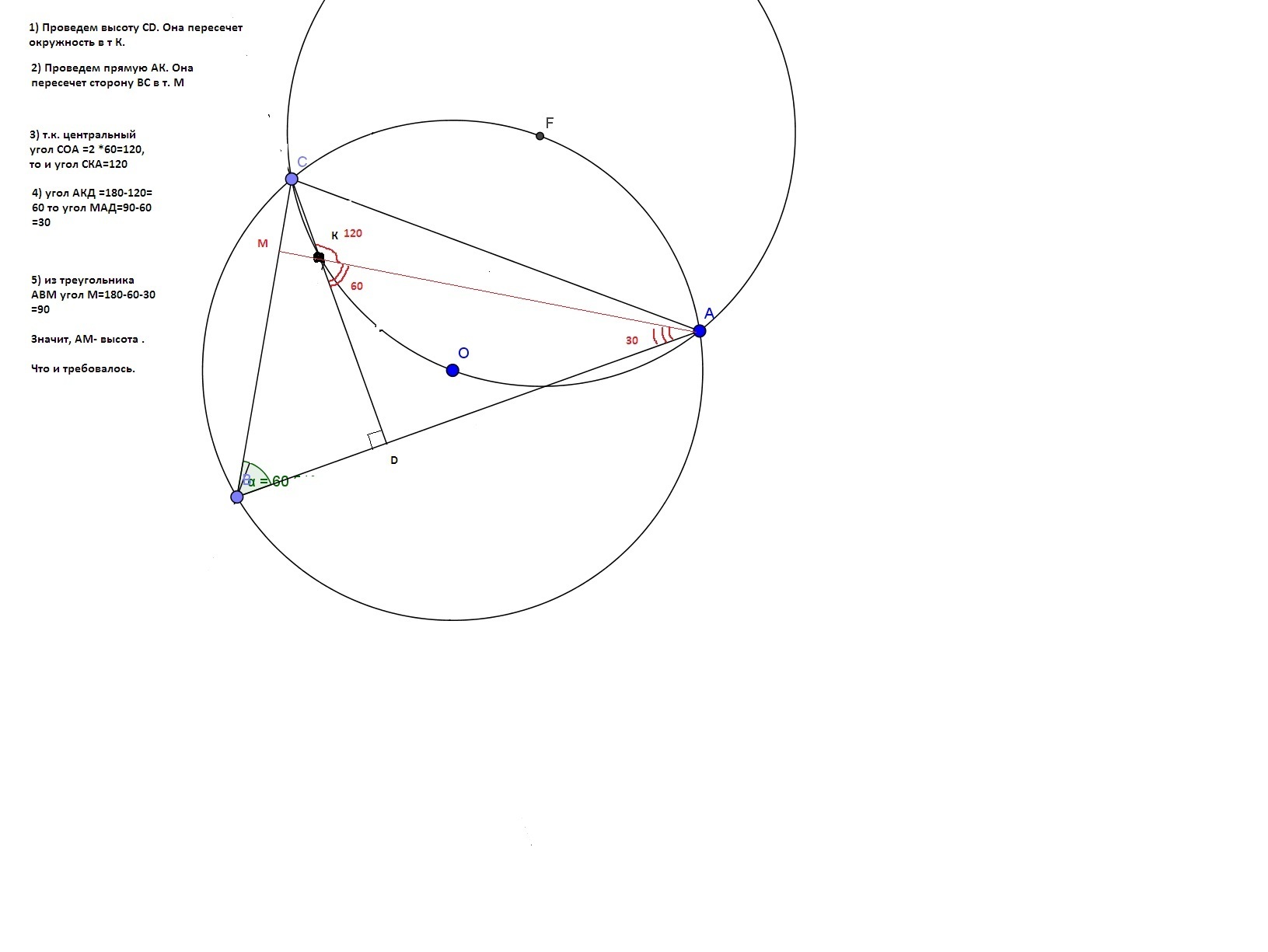
Ответил nabludatel00
0
"Но если прямая СD пересекается с окружностью вне треугольника, картинка же получается другая " - конечно другая! Тогда треугольник будет тупоугольным. Что не соответствует условию. Я ж говорил уже.
Ответил nabludatel00
0
Вы совершенно правы по решению. Этот вариант мне даже в голову не пришел. Запомним очередной мой косяк. Трудно мне тягаться с такими монстрами.... Это у меня так, для гимнастики мозгов. Не все ж время работать руками и машины разгружать. Я и формул многих не знаю, а некоторые названия, которыми здесь люди оперируют, впервые слышу.
Ответил nabludatel00
0
Мое решение, как неоптимальное, предлагаю удалить..
Ответил hote
0
удалять? или исправите?
Ответил nabludatel00
0
Исправлять не буду, не я ж предложил то решение.Думаю,пусть висит, чтоб можно было пересматривать решение и видеть неоптимальное и оптимальное. Пусть будет на будущее. Если топикстартер не против.
Новые вопросы
Математика,
2 года назад
Математика,
8 лет назад
Математика,
8 лет назад
Математика,
9 лет назад
Химия,
9 лет назад