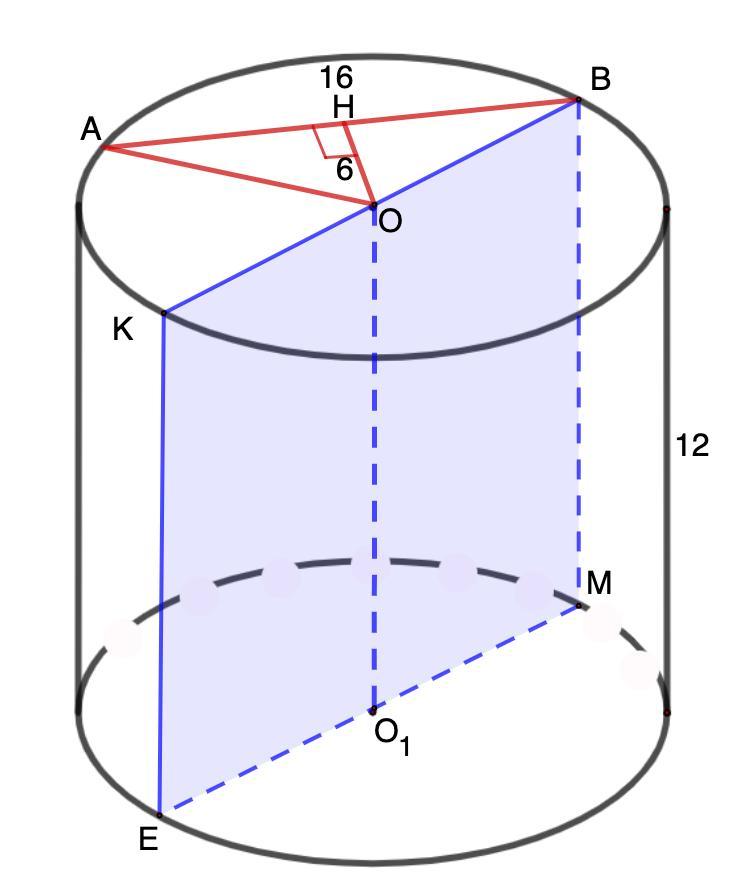
Дан цилиндр, высота которого равна 12. В верхнем основании цилиндра проведена хорда AB = 16. Расстояние от данной хорды до центра O верхнего основания цилиндра равно 6. Найдите площадь осевого сечения рассматриваемого цилиндра. Рисунок обязателен.

Ответ:

Площадь осевого сечения рассматриваемого цилиндра равна 240 ед.²

Объяснение:

Требуется найти площадь осевого сечения рассматриваемого цилиндра.

Дано: цилиндр;

ВМ = 12 - высота;

AB = 16 - хорда;

ОН = 6;

Найти: S (EKBM)

Решение:

1. Рассмотрим ΔОНВ.

• Расстояние от точки до прямой - перпендикуляр, опущенный из точки на прямую.

⇒ ΔОНВ - прямоугольный.

• Если радиус перпендикулярен хорде, то он проходит через ее середину.

⇒ АН = НВ = 16 : 2 = 8

По теореме Пифагора найдем радиус ОВ:

ОВ² = НВ² + ОН² = 64 + 36 = 100

ОВ = √100 = 10

2. Рассмотрим ЕКВМ - прямоугольник.

ВМ = 12; КВ = 2 ОВ = 20.

• Площадь прямоугольника равна произведению смежных сторон.

S (ЕКВМ) = ВМ · КВ = 12 · 20 = 240 (ед.²)

Площадь осевого сечения рассматриваемого цилиндра равна 240 ед.²