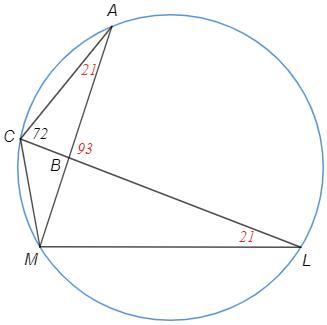
Дан четырехугольник CALM, вершины которого лежат на окружности. Диагонали CL и AM пересекаются в точке B. ∠ACL = 72*, ∠LCM + ∠LMC = 159*.
Найдите градусную меру угла ∠ABL.

Сумма внутренних углов треугольника 180°.

△CLM: ∠CLM+∠LCM+∠LMC =180° => ∠CLM =180°-159° =21°

Вписанные углы, опирающиеся на одну дугу, равны.

∠CAM=∠CLM=21° (вписанные, опираются на дугу CM)

Внешний угол треугольника равен сумме внутренних, не смежных с ним.

△ABC: ∠ABL =∠ACB+∠CAB =∠ACL+∠CAM =72°+21° =93°