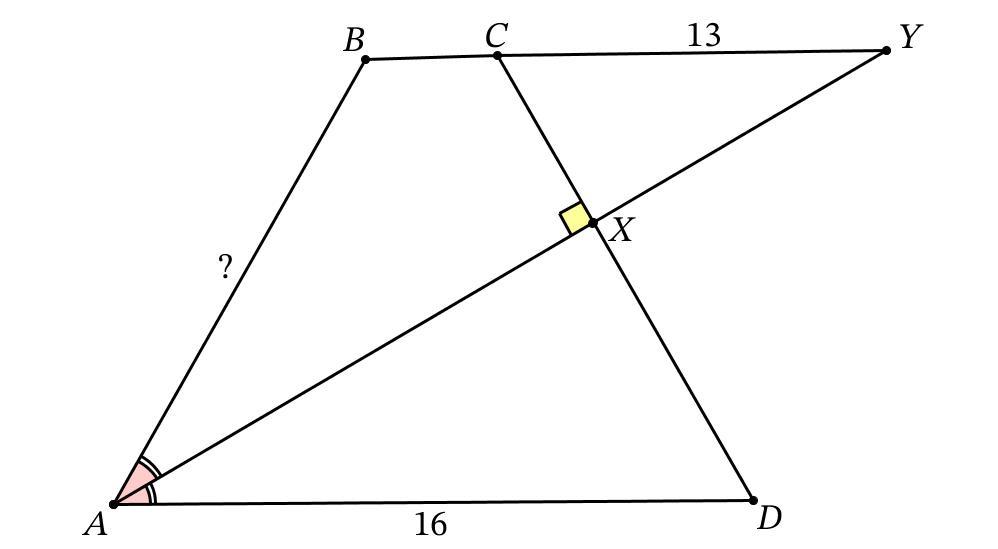
Дан четырёхугольник ABCD, в котором AD∥BC. Биссектриса угла A пересекает сторону CD в точке X, а продолжение стороны BC за точку C — в точке Y. Оказалось, что ∠AXC=90∘.



Найдите длину отрезка AB, если известно, что AD=16 и CY=13.

Ответ:

15, Вроде так, но не уверен

Пошаговое объяснение:

можно продлить AB и CD до пересечения в точке E. Получается треугольник EAD, в нём прямая AX одновременно высота и биссектриса , значит этот треугольник равнобедренный и

AE=AB+BE=AD=16

Треугольник EBC тоже равнобедренный, поэтому EB=BC

С учётом этого , значит

AB+BC=16

BC=16-AB

Дальше:

Так как AD параллельно BC, то треугольник ABY тоже равнобедренный, значит

AB=BC+CY=BC+13

У нас получилось выражение

AB=(16-AB)+14

2AB=16+14=30

AB=30:2=15