Дам 30 баллов)
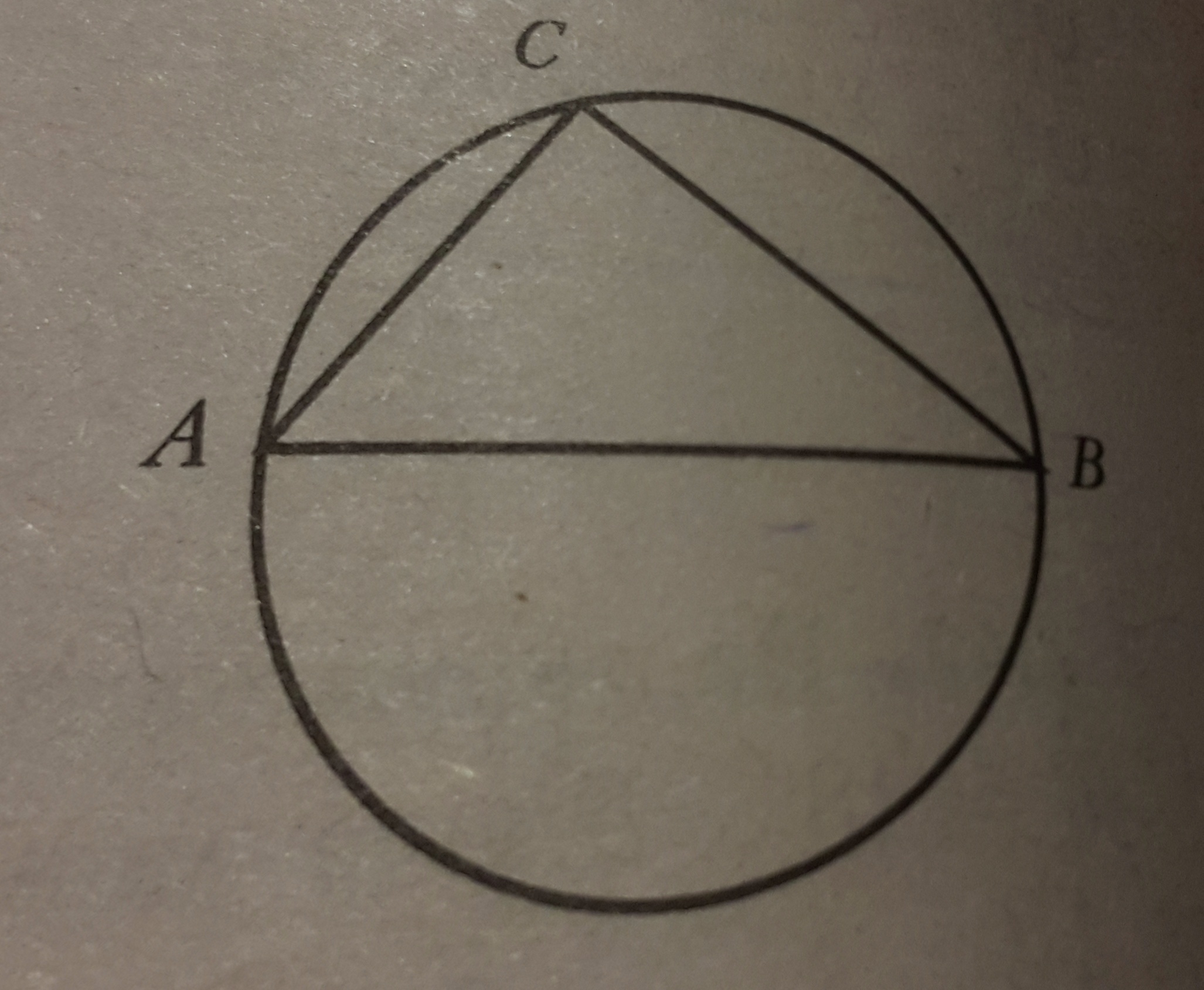
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружиoсти равен 15. Найдите AC, если BC = 24.

Если центр окружности лежит на стороне треугольника, то тогда только на его середине.
В таком случае сторона AB является диаметром описанной окружности, а ΔACB - прямоугольный, т.к. ∠С - вписанный, опирающийся на диаметр.
AB = 2R = 2·15 = 30.
По теореме Пифагора:
AC = √(AB² - BC²) = √(30² - 24²) = √(900 - 576) = √324 = 18.
Ответ: AC = 18.