ДАМ 25 БАЛЛОВ!
Решить задачу: круг вписан в трапецию, боковые стороны которой равны как 18см и 20 см. Найти среднюю линию трапеции
Ответы на вопрос
Ответил ivanproh1
1
Ответ:
Средняя линия равна 19см.
Объяснение:
Если в трапецию вписана окружность, то сумма ее оснований равна сумме боковых сторон. =>
Средняя линия равна (BC+AD)/2 = (AB+CD)/2 = (18+20)/2 = 19см.
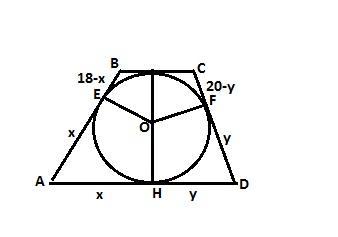
Или так: вершины А, В, С и D - точки, из которых проведены касательные к вписанной в трапецию окружности (стороны трапеции). Отрезки касательных, проведенных из одной точки, равны =>
AD = x + y. (1)
BC = (18-x) + (20-y). (2)
Сложим (1) и (2) и получим: AD+BC = 18+20. =>
Средняя линия равна (18+20)/2 = 19.
Приложения:
Новые вопросы
Английский язык,
1 год назад
Українська мова,
1 год назад
Математика,
1 год назад
Физика,
1 год назад
Другие предметы,
6 лет назад