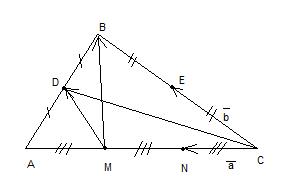
D и E- середины сторон AB и BС треугольника ABC, точки М и N лежат на AC, причем АМ=MN=NC
Вектор CN= вектору а
Вектор CE=вектору б
Выразить вектор CD, вектор MB, вектор MD через эти векторы. Спасибо за помощь!!!
Ответы на вопрос
Ответил Suasore
0
По правилу треугольника CD=CB+BD, CD=CA+AD.
Складываем эти равенства и получаем:
2CD=CB+CA+BD+AD. Т.к. точка D - середина стороны АВ, то AD+BD=0. Тогда
2CD=CB+CA, CD=1/2(CB+CA)=1/2(2b+3a)=b+3/2a
MB=MC+CB. Т.к. MN=NC=-a, то МС=-2а,
MB=-2а+2b
MD=MC+CD=-2a+(b+3/2a)=b-1/2a
Везде надо поставить знаки векторов, не забудь.
Складываем эти равенства и получаем:
2CD=CB+CA+BD+AD. Т.к. точка D - середина стороны АВ, то AD+BD=0. Тогда
2CD=CB+CA, CD=1/2(CB+CA)=1/2(2b+3a)=b+3/2a
MB=MC+CB. Т.к. MN=NC=-a, то МС=-2а,
MB=-2а+2b
MD=MC+CD=-2a+(b+3/2a)=b-1/2a
Везде надо поставить знаки векторов, не забудь.
Приложения:
Новые вопросы