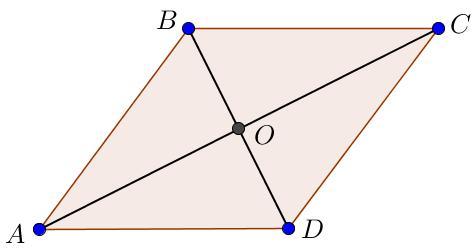
Діагоналі ромба дорівнюють 12 см.;12√3см. Знайти гострий кут ромба.
Ответы на вопрос
стороны равны между собой у ромба
диагонали ромба в точке пересечения делятся пополам и делят сам ромб на 4 равных прямоугольных треугольника
также диагонали являются биссектрисами углов .
Сумма углов при одной стороне равна 180 °, а противоположные углы равны между собой
синус равен отношению противоположного катета к гипотенузе
косинус равен отношени
ю прилежащего катета к гипотенузе.
Это вся теория ,которую нужно знать для этой задачи
допустим дан ромб ABCD, в нем проведены две диагонали АС и BD. точка пересечения О
расмотрим любой маленький треугольник ,допустим АОВ ( угол О =90°) половины диагоналей ромба это катеты
12:2=6см - АО
12√3:2=6√3 см -- ВО
найдем гипотенузу ВА с помощью теоремы Пифагора
квадрат гипотенузы равен сумме квадратов катетов
ВА²=ВО²+АО²
ВА=√(ВО²+АО²)
√(6²+(6√3 )²=√ (36+36×3)=√(36×4)=6×2=12 см -гипотенуза
sinA=6/12=1/2 -> 30°
sinB=6√3 /12= √3/2 -> 60°
умножим на два ,чтобы найти углы в ромбе
2×30=60° угол А
2×60=120° угол В
угол А острый так как меньше 90°