(d^2*z/d*x*d*y)+y((d*z/(d*x)+x(d*z/d*y)+x*y*z=0
z=х*e^-(х^2+y^2/2)
Проверить удовлетворяет ли функция дифференциальному уравнению
Приложения:
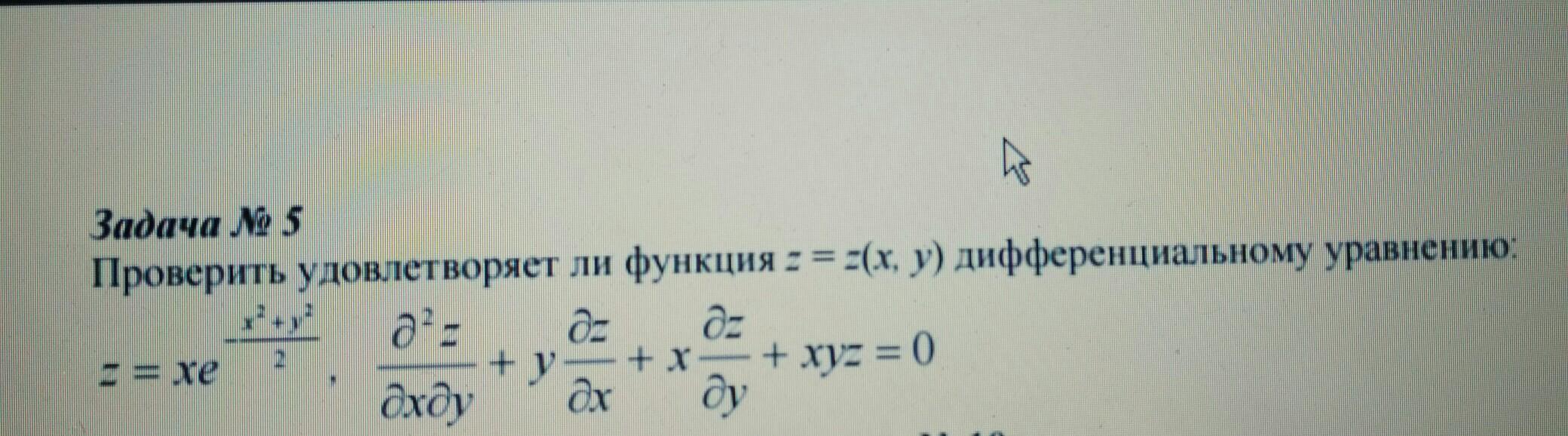
Ответы на вопрос
Ответил NNNLLL54
0
Заданная функция удовлетворяет дифференциальному уравнению.
Новые вопросы
Русский язык,
1 год назад
Алгебра,
7 лет назад
Алгебра,
7 лет назад
История,
8 лет назад
Математика,
8 лет назад