Алгебра, вопрос задал 030323 , 7 лет назад

cos2p/7+cos4p/7+cos6p/7=-1/2 докажите тождество.

Ответы на вопрос

Ответил Аноним

$cosdfrac{2pi}{7}+cosdfrac{4pi}{7}+cosdfrac{6pi}{7}=dfrac{2sindfrac{pi}{7}}{2sindfrac{pi}{7}}left(cosdfrac{2pi}{7}+cosdfrac{4pi}{7}+cosdfrac{6pi}{7}right)=\ \ \ =dfrac{1}{2sindfrac{pi}{7}}left(2sindfrac{pi}{7}cosdfrac{2pi}{7}+2sindfrac{pi}{7}cosdfrac{4pi}{7}+2sindfrac{pi}{7}cosdfrac{6pi}{7}right)=\ \ \ =dfrac{1}{2sindfrac{pi}{7}}left(sindfrac{3pi}{7}-sindfrac{pi}{7}+sindfrac{5pi}{7}-sindfrac{3pi}{7}+sinpi-dfrac{5pi}{7}right)=\\\= -dfrac{1}{2sindfrac{pi}{7}}cdot left(-sindfrac{pi}{7}right)=-dfrac{1}{2}$

Ответил antonovm

Класс !

Ответил antonovm

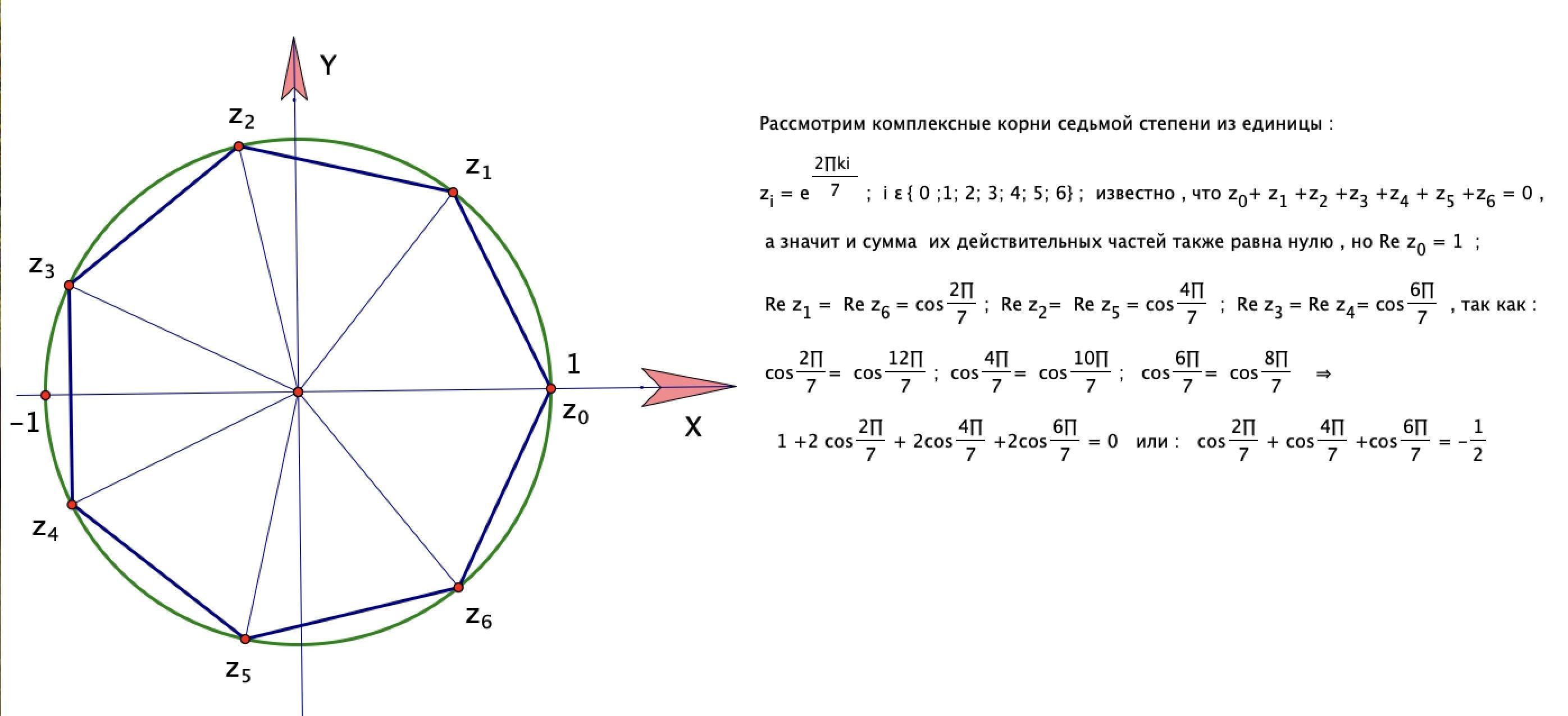
Решение не совсем школьное , но верное , использованы

свойства корней n- ой степени из единицы ( комплексных

корней )

Приложения:

Ответил antonovm

можно еще использовать , что сумма векторов с началом в точке (0 ; 0) , концы которых в вершинах правильного n - угольника , вписанного в единичную окружность равна 0 , но тогда равна нулю сумма их первых координат , а это и есть сумма удвоенных косинусов и единицы

Ответил antonovm

примитивные корни из 1 являются степенями z1 , их сумму легко найти по формуле для геометрической прогрессии : S = (z1^7 - 1) /(z1 - 1) = 0 - это пояснение , почему сумма 6 чисел равна 0

Ответил antonovm

7 чисел

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

Помогите, пожалуйста!!! Put the comparative or superlative form of the adjectives in brackets. The sinking of the Titanic is one of 1) ... (famous) shipwreck stories of all time. The Titanic was...

Русский язык, 1 год назад

Способы выражения обстоятельств???)...

Математика, 7 лет назад

Напишите пожалуйста как решить дробь 8 16 ⁻⁻ + ⁻⁻ = 12 21...

Геометрия, 7 лет назад