Алгебра, вопрос задал SVETKAKONVETKA , 7 лет назад

что нибудь, с решением 11 класс

Приложения:

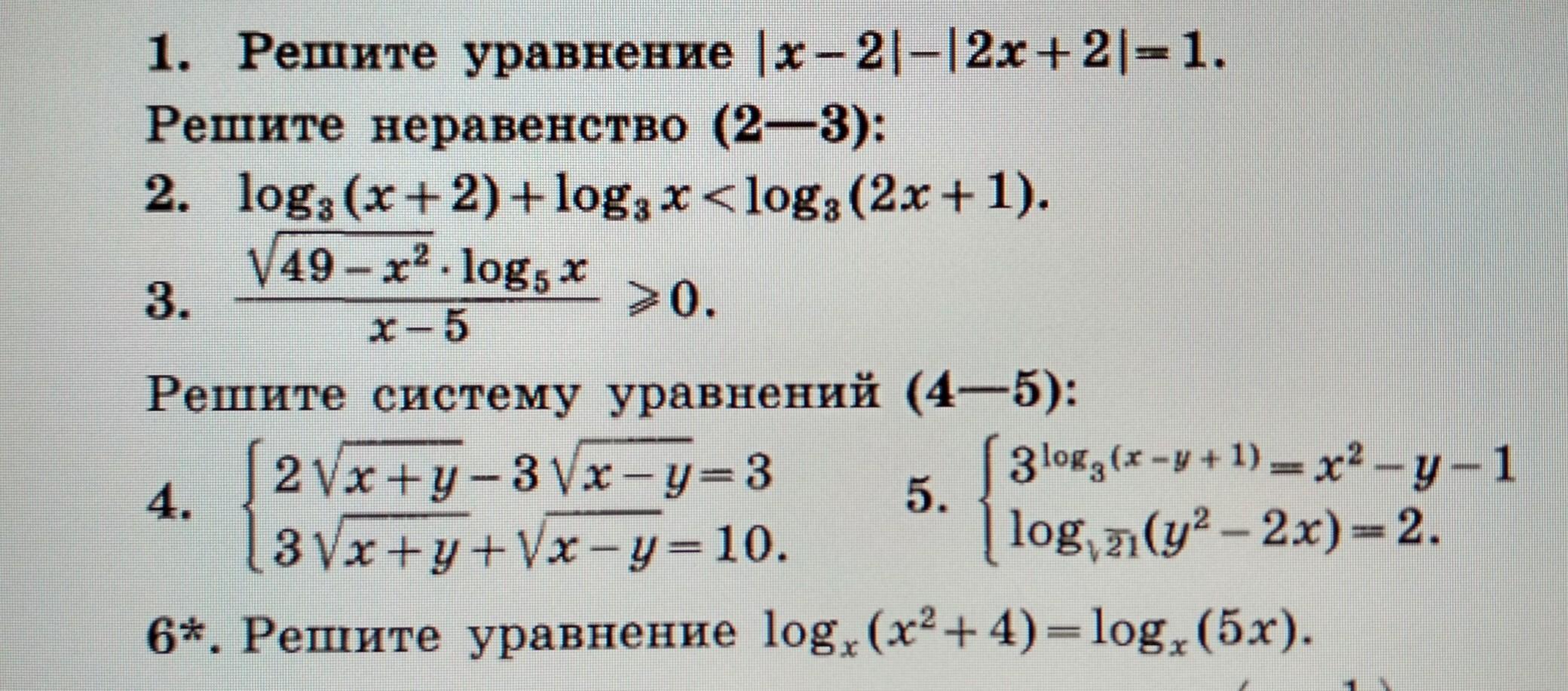
Ответы на вопрос

Ответил Universalka

0

$4)left { {{2sqrt{x+y}-3sqrt{x-y} =3 } atop {3sqrt{x+y} +sqrt{x-y}=10 }|*3} right.\\+left { {{2sqrt{x+y}-3sqrt{x-y} =3 } atop {9sqrt{x+y}+3sqrt{x-y}=30 }} right.\ 11sqrt{x+y}=33\ sqrt{x+y}=3\x+y=9\2*3-3sqrt{x-y} =3\3sqrt{x-y}=3\sqrt{x-y}=1\x-y=1$

$+left { {{x+y=9} atop {x-y=1}} right. \------\2x=10\x=5\y=9-5=4$

Ответ : (5 ; 4)

$5)left { {{3^{log_{3}(x-y+1) }=x^{2}-y+1} atop {log_{sqrt{21}}(y^{2}-2x)=2}} right.\\left { {{x-y+1=x^{2}-y+1 } atop {y^{2} -2x=21}} right.\\left { {{x^{2}-x=0 } atop {y^{2}=21+2x }} right.\\left { {{x(x-1)=0} atop {y^{2}=21+2x }} right.$

$x_{1}=0\\y^{2}=21+2*0=21\\y_{1} =-sqrt{21}\\y_{2}=sqrt{21}\\x_{2}=1\\y^{2}=21+2*1=23\\y_{3}=-sqrt{23}\\y_{4}=sqrt{23}$

y₁ и y₄ - не подходят

Ответ : (0 ; - √21) , (1 ; - √23)

6) ОДЗ : x > 0 , x ≠ 1

$log_{x}(x^{2}+4)=log_{x}(5x)\\x^{2}+4=5x\\x^{2}-5x+4=0\\x_{1}=4\\x_{2}=1$

x₂ - не подходит

Ответ : 4

Ответил Universalka

0

Если время позволяет, то могу ещё решить .

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Українська мова, 1 год назад

Твір - роздум " Навіщо вивчати українську мову?"...

Русский язык, 1 год назад

Маленькое дело лучше большого безделья морфологический разбор прилагательного...

Химия, 7 лет назад

m(K)=78г v(O2)=? K+O2=...

Химия, 7 лет назад

Який тип хімічного звязку HNO3...

География, 8 лет назад

какие районы нашей страны самые большие по численности населения...

Геометрия, 8 лет назад

Помогите, пожалуйста.. В параллелограмме ABCD угол А равен 42 гр.. Найдите величину угла D. Нужно только решение. Спасибо.