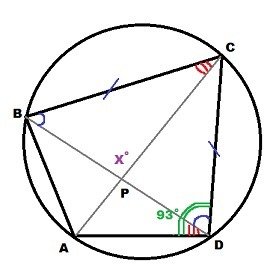
Четырёхугольник ABCD вписан в окружность, причём ВС = СD. Известно, что угол ADC=93 градуса. Найдите, под каким острым углом пересекаются диагонали этого четырёхугольника. Ответ дайте в градусах.

ВС = СD ⇒  ΔBCD - равнобедренный   ⇒  ∠CBD = ∠CDB

∠BDA = ∠BCA   опираются на одну дугу  ∪BA ⇒
∠CBD + ∠BCA = ∠CDB + ∠BDA = ∠ADC = 93°   ⇒
В треугольнике ΔBCP :
∠BPC = 180° - (∠CBP + ∠BCP) = 180°-93° = 87° < 90°  ⇒ острый

Ответ: диагонали пересекаются под острым углом 87°