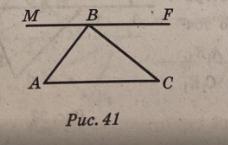
Через вершину В трикутника АВС проведено пряму MF, паралельну прямій АС (рис. 41). Величини кутів АВМ, АВС i CBF відносяться як 3:5:2. Знайдіть кути трикутни- ка ABC.
Приложения:
Ответы на вопрос
Ответил liftec74
1
Ответ: ∡ВАС=54°, ∡АВС=90°, ∡ВСА=36°
Объяснение:
1. Найдем ∡АВМ, ∡АВС i ∡CBF .
∡АВМ+ ∡АВС + ∡CBF=180°
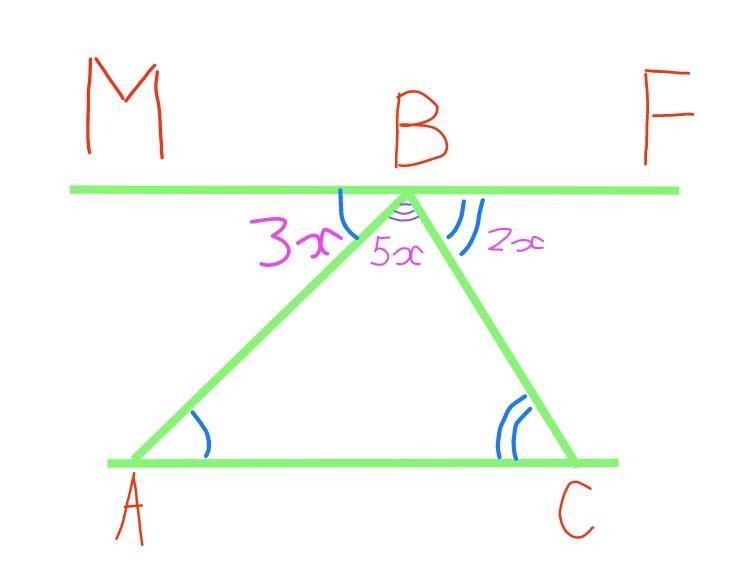
∡АВМ=3x, ∡АВС=5x i ∡CBF=2x
=> 3x+5x+2x=10x=180°
=> x=18°
=> ∡АВМ=3*18°=54°, ∡АВС=5*18°=90° i ∡CBF=2*18°=36°
∡CBF i ∡BCA - накрест лежащие. Кроме того они образованы при пересечении параллельных прямых АС и MF прямой ВС.
Значит ∡CBF =∡BCA=36°
Аналогично ∡ВАС=∡АВМ=54°
Ответил egor2009zolozhckov
0
Відповідь: АВС=90°
ВАС=54°
ВСА=36°
Нижче зображення з малюнком.
З умови нам дано відношення цих кутів. Складемо рівняння
3х+5х+2х=180°
х=18°
АВМ=54°
АВС=90°
СВF=36°
кут АВМ та ВАС рівні, бо вони різносторонні.
кут СВF та ВСА рівні, бо різносторонні.
Приложения:
Новые вопросы
Биология,
2 месяца назад
Математика,
2 месяца назад
История,
2 месяца назад
Английский язык,
2 месяца назад
Химия,
6 лет назад