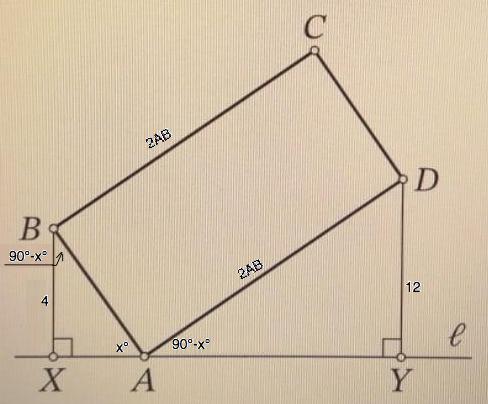
Через вершину A прямоугольника ABCD проведена прямая ℓ, как изображено на рисунке. Из точек B и D опущены перпендикуляры BX и DY на прямую ℓ. Найдите длину отрезка XY, если известно, что BX=4, DY=12, BC=2AB.

СРОЧНО

Ответ: 14 (ед. длины)

Объяснение:

Угол ХАY - развернутый=180°.

Угол ВАD=90°( АВСD - прямоугольник),

∠ВАХ+у∠DAY=180°-90°=90°.

Примем ∠ВАХ=х°

Тогда ∠DAY=90°-x°.

∠ХВА=90°-х°(т.к. сумма острых углов прямоугольного треугольника – 90°).

∠АВХ=∠DAY =>

∆ АВХ~∆ ADY по острому углу.

AD=BC=2AB. =>

k=AD:AB=2 =>

AY=2BX=2•4=8;

DY=2XA=> XA=12:2=6.

XY=XA+AY=6+8=14 (ед. длины).