Через точки Р и Q прямой PQ проведены прямые, перпендикулярные к плоскости α и пересекающие ее соответственно в точках Р1 и Q1. Найдите P1Q1, если PQ = 15 см, РР1 = — 21,5 см, QQ1=33,5 см.
Ответы на вопрос
Ответил KuOV
0
Возможны два случая расположения отрезка PQ и плоскости α.
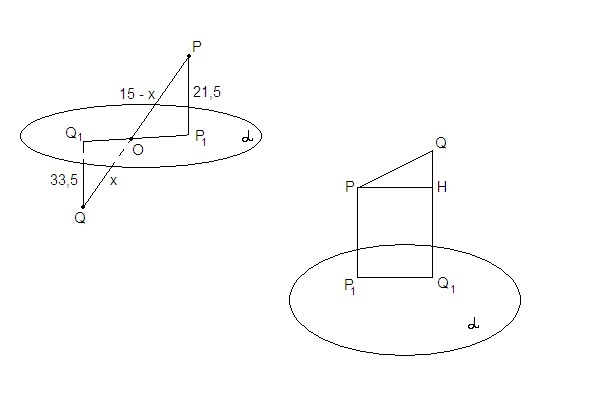
1. Отрезок пересекает плоскость. (рис.1)
Пусть QO = x, OP = 15 - x
ΔOQQ₁ подобен ΔOPP₁ по двум углам (∠OQ₁Q = ∠ОР₁Р = 90°, углы при вершине О равны как вертикальные)
x/(15 - x) = 33,5/21,5 = 67/43
43x = 1005 - 67x
110x = 1005
x = 1005/110 = 201/22 = 9 3/22
Но это невозможно, т.к. OQ - гипотенуза в прямоугольном треугольнике OQQ₁ и она не может быть меньше катета QQ₁.
2. Отрезок PQ не пересекает плоскость α. (рис. 2)
Q₁Q⊥α и Р₁Р⊥α, ⇒ Q₁Q ║ Р₁Р значит точки Q₁, Q, Р₁ и Р лежат в одной плоскости.
Q₁QРР₁ - прямоугольная трапеция.
Проведем РН⊥Q₁Q. Тогда PP₁Q₁H - прямоугольник.
Q₁H = PP₁ = 21,5, ⇒ HQ = 33,5 - 21,5 = 12 см
ΔPQH: ∠PHQ = 90°, по теореме Пифагора
РH = √(PQ² - QH²) = √(15² - 12²) = √81 = 9 см
P₁Q₁ = PH = 9 см
1. Отрезок пересекает плоскость. (рис.1)
Пусть QO = x, OP = 15 - x
ΔOQQ₁ подобен ΔOPP₁ по двум углам (∠OQ₁Q = ∠ОР₁Р = 90°, углы при вершине О равны как вертикальные)
x/(15 - x) = 33,5/21,5 = 67/43
43x = 1005 - 67x
110x = 1005
x = 1005/110 = 201/22 = 9 3/22
Но это невозможно, т.к. OQ - гипотенуза в прямоугольном треугольнике OQQ₁ и она не может быть меньше катета QQ₁.
2. Отрезок PQ не пересекает плоскость α. (рис. 2)
Q₁Q⊥α и Р₁Р⊥α, ⇒ Q₁Q ║ Р₁Р значит точки Q₁, Q, Р₁ и Р лежат в одной плоскости.
Q₁QРР₁ - прямоугольная трапеция.
Проведем РН⊥Q₁Q. Тогда PP₁Q₁H - прямоугольник.
Q₁H = PP₁ = 21,5, ⇒ HQ = 33,5 - 21,5 = 12 см
ΔPQH: ∠PHQ = 90°, по теореме Пифагора
РH = √(PQ² - QH²) = √(15² - 12²) = √81 = 9 см
P₁Q₁ = PH = 9 см
Приложения:
Новые вопросы