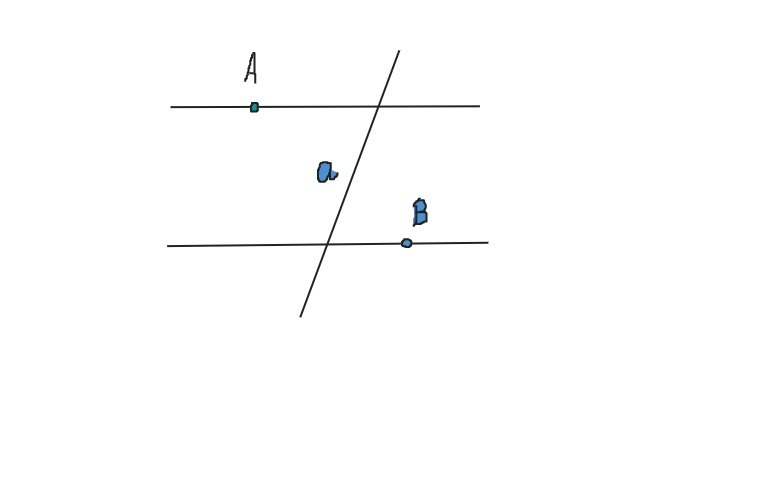
Через точки А и В можно провести две параллельные прямые (одна проходит через точку А, другая – через точку B), которые пересекают прямую а. Докажите, что точки А и В и прямая а лежат в одной плоскости.
Ответы на вопрос
Ответил ЗельеварСнейп
0
Можно доказать через теорему и аксиому.
По теореме 2 "через 2 пересекающиеся прямые проходит плоскость и при том только 1".
Рассмотрим прямую с точкой А и прямую а. Они пересекаются, следовательно, принадлежат одной плоскости.
Рассмотрим прямую с точкой В и прямую а. Они пересекаются, следовательно, лежат в одной плоскости.
Две прямые в пространстве называются параллельными, если лежат в одной плоскости и не пересекаются. По условию они параллельны, следовательно лежат в одной плоскости, как и лежат в одной плоскости с прямой а.
Получается, три прямые лежат в одной плоскости.
Точки А и В лежат в этой же плоскости, потому что по аксиоме 2 " если прямая лежит в этой плоскости, то и все точки прямой лежат в этой же плоскости"
точка А лежит на прямой
Точка В лежит на прямой.
Следовательно, они принадлежат одной плоскости.
чтд
По теореме 2 "через 2 пересекающиеся прямые проходит плоскость и при том только 1".
Рассмотрим прямую с точкой А и прямую а. Они пересекаются, следовательно, принадлежат одной плоскости.
Рассмотрим прямую с точкой В и прямую а. Они пересекаются, следовательно, лежат в одной плоскости.
Две прямые в пространстве называются параллельными, если лежат в одной плоскости и не пересекаются. По условию они параллельны, следовательно лежат в одной плоскости, как и лежат в одной плоскости с прямой а.
Получается, три прямые лежат в одной плоскости.
Точки А и В лежат в этой же плоскости, потому что по аксиоме 2 " если прямая лежит в этой плоскости, то и все точки прямой лежат в этой же плоскости"
точка А лежит на прямой
Точка В лежит на прямой.
Следовательно, они принадлежат одной плоскости.
чтд
Приложения:
Новые вопросы
Геометрия,
2 года назад
Геометрия,
2 года назад
Математика,
8 лет назад
Физика,
8 лет назад
Обществознание,
9 лет назад
Математика,
9 лет назад