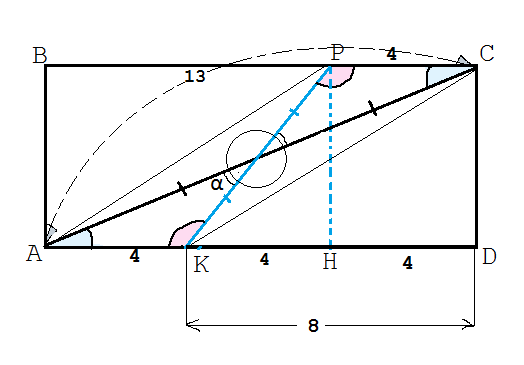
Через середину о диагонали ac прямоугольника abcd проведена прямая, пересекающая стороны BC и AD в точках P и K соответственно.
1) Докажите, что APCK - паралелограм.
2) Найдите площадь APCK, если AK=4, KD=8 и AC=13.
3) Найдите PK.
4) С помощью микро калькулятора найдите угол AOK.
Ответы на вопрос
Ответил Hrisula
20
1)Треугольники АОК и РОС равны по трем углам:
∠АКР=∠КРС,∠РСА=∠САК как накрестлежащие при параллельных прямых ВС и АD и секущих, углы при О равны, как вертикальные.
Следовательно, равны и треугольники АОВ и КОС по двум сторонам и углу между ними: АО=ОС, КО=ОР, углы при О - вертикальные. ⇒
РС=АК, АР=КС.
Четырехугольник, в котором противоположные стороны попарно равны - параллелограмм.
-----
2) Площадь АРСК можно вычислить произведением высоты на основание. Высота этого параллелограмма, проведенная из вершины С к АК = СД.
S =ah=AK*CD
CD - катет прямоугольного треугольника с отношением сторон АС:АD:DC=13:12:х. Треугольник из Пифагоровых троек, и СD=5 ( проверить можно по т.Пифагора)
S=4*5=20 (ед.площади)
-----
3) РК найдем из прямоугольного треугольника КРН, где РН⊥КD; РН=СD=5
По т.Пифагора
КР= √(КН² +РН² )=√41
----
4) Одна из формул для нахождения площади параллелограмма S=0,5*d1*d2*sin(α)
20=0,5*AC*KP*sin α
sin α=40:(13*√41)=40: (13*6,403) ≈ 0,4805
По таблице синусов это синус угла 28°43'
∠АКР=∠КРС,∠РСА=∠САК как накрестлежащие при параллельных прямых ВС и АD и секущих, углы при О равны, как вертикальные.
Следовательно, равны и треугольники АОВ и КОС по двум сторонам и углу между ними: АО=ОС, КО=ОР, углы при О - вертикальные. ⇒
РС=АК, АР=КС.
Четырехугольник, в котором противоположные стороны попарно равны - параллелограмм.
-----
2) Площадь АРСК можно вычислить произведением высоты на основание. Высота этого параллелограмма, проведенная из вершины С к АК = СД.
S =ah=AK*CD
CD - катет прямоугольного треугольника с отношением сторон АС:АD:DC=13:12:х. Треугольник из Пифагоровых троек, и СD=5 ( проверить можно по т.Пифагора)
S=4*5=20 (ед.площади)
-----
3) РК найдем из прямоугольного треугольника КРН, где РН⊥КD; РН=СD=5
По т.Пифагора
КР= √(КН² +РН² )=√41
----
4) Одна из формул для нахождения площади параллелограмма S=0,5*d1*d2*sin(α)
20=0,5*AC*KP*sin α
sin α=40:(13*√41)=40: (13*6,403) ≈ 0,4805
По таблице синусов это синус угла 28°43'
Приложения:
Новые вопросы
Английский язык,
1 год назад
Русский язык,
1 год назад
Математика,
1 год назад
Математика,
7 лет назад