БУДЬ ЛАСКА ДОПОМОЖІТЬ
розв'яжіть рівняння
6arcsin(1-x-x²)<pi

​

6arcsin(1 – x - x²) < pi,

arcsin(1 – x - x²) < (pi/6),

1 – x - x² < 0.5,

x² + x – 0.5 > 0.

Решаем уравнение x² + x – 0.5 = 0,

D = 1 – 4*1*(-0,5) = 3, √D = ±√3,

x1 = (-1 - √3)/2 ≈ -1,366025,

x2 = (-1 + √3)/2 ≈ 0,366025.

Находим предельные значения переменной из условия, что функция синуса для угла, меньшего (pi/6), имеет предел (-1).

1 – x - x² = -1,

x² + x – 2 = 0,

D = 1 – 4*1*(-2) = 9, √D = ±3,

x1 = (-1 - 3)/2 = -2,

x2 = (-1 + 3)/2 = 1.

Суммируя полученные результаты, получаем ответ в виде двух промежутков.

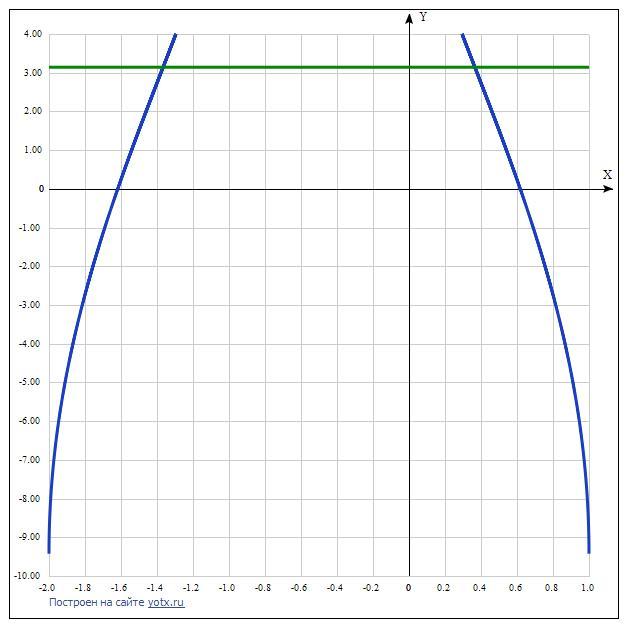
-2 ≤ x < (-1 - √3)/2,

(-1 + √3)/2 < x ≤ 1.