Геометрия, вопрос задал Аноним , 6 лет назад

будь ласка допоможіть

Приложения:

Аноним: я 1 варіант

Аноним: забула написати

Ответы на вопрос

Ответил NNNLLL54

2

Ответ:

1 вариант.

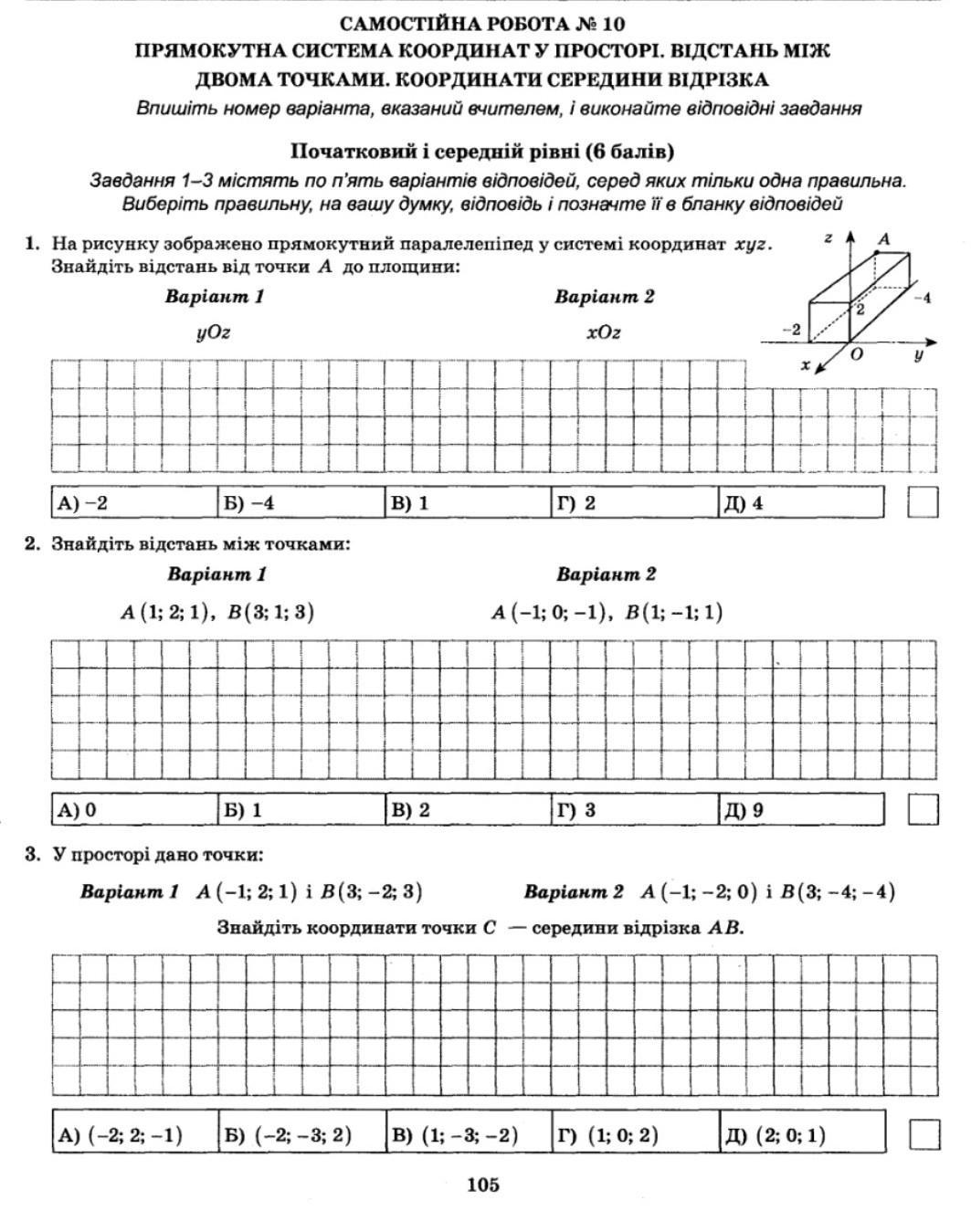
1) Если из точки А в прямоугольном параллелепипеде провести перпендикуляр на плоскость УOZ (фронтальная плоскость на рисунке) , то основанием перпендикуляра на этой плоскости будет точка А1 . Длина перпендикуляра АА1 , который получается параллельным оси ОХ, и будет искомым расстоянием , АА1=4 , так как координаты точки А(-4;-2;2) , а координаты точки А1(0;-2;2) .

Ответ: Д) .

2) Расстояние между точками вычисляется по формуле

$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}$ .

$A(1;2;1)\ ,\ B(3;1;3)\\\\AB=\sqrt{(3-1)^2+(1-2)^2+(3-1)^2}=\sqrt{2^2+1^2+2^2}=\sqrt9=3$

Ответ: Г) .

3) Координаты середины отрезка равны полусумме координат концов этого отрезка .

$A(-1;2;1)\ ,\ B(3;-2;3)\\\\x_{C}=\dfrac{-1+3}{2}=1\ \ ,\ \ y_{C}=\dfrac{2-2}{2}=0\ ,\ \ z_{C}=\dfrac{1+3}{2}=2\\\\C(\, 1\, ;\, 0\, ;2\, )$

Ответ: Г) .

Приложения:

Arwergnis: Мне помогите пожалуйста вопрос в профиля

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

сочинение на тему подготовка к новому году...

Русский язык, 1 год назад

Как пишутся строчные буквы...

История, 6 лет назад

1860-70 жыл көтеріліс басталу себебі...

Информатика, 6 лет назад

Вопрос : можно ли пройти таким путем: A - B - F ? Вот технически и самая короткая дорога... Или я ошибаюсь? Поясните, пожалуйста. P. S условия : Нужно найти длину кратчайшего простого пути между...

Математика, 8 лет назад

Выполните деление(28а-12d)делить на 4...

Математика, 8 лет назад

решите уравнение -2 (x-6)=0 -y (y+8)(y-1)=0...