боковая сторона равнобедренного треугольника равна 10 см а один из углов 120 градусов. постройте треугольник симметричный данному треугольнику относительно середины его основания. Определите периметр и меньшую диагональ полученного четерехугольника!
Хелп помогите срочно надо!!!!
Ответы на вопрос
Ответил Hrisula
0
Определение
Фигура называется симметричной относительно точки О, если для любой точки фигуры точка, симметричная ей, также принадлежит данной фигуре. Точка О называется центром симметрии, а фигура обладает центральной симметрией.
------------------------
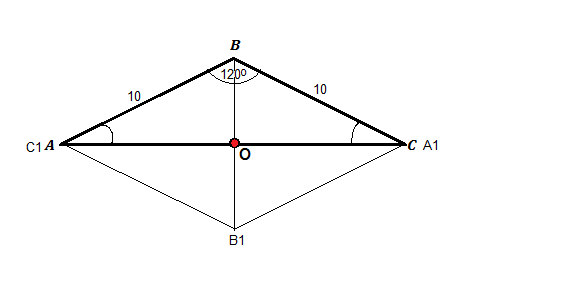
Обозначим середину основания данного равнобедренного треугольника О.
Треугольник, симметричный данному относительно точки О - равнобедренный треугольник А₁В₁С₁ со сторонами 10 см.
Получившийся четырехугольник - ромб.
Периметр его 10*4=40 см
Острые углы треугольника АВС=(180º-120º):2=30º
Острый угол ромба ∠BAC+ ∠В₁С₁А₁=30°+30°=60°.
Половина меньшей диагонали противолежит углу 30° и равна АВ:2=5 см
Вся диагональ ВВ₁=5*2=10 см
Фигура называется симметричной относительно точки О, если для любой точки фигуры точка, симметричная ей, также принадлежит данной фигуре. Точка О называется центром симметрии, а фигура обладает центральной симметрией.
------------------------
Обозначим середину основания данного равнобедренного треугольника О.
Треугольник, симметричный данному относительно точки О - равнобедренный треугольник А₁В₁С₁ со сторонами 10 см.
Получившийся четырехугольник - ромб.
Периметр его 10*4=40 см
Острые углы треугольника АВС=(180º-120º):2=30º
Острый угол ромба ∠BAC+ ∠В₁С₁А₁=30°+30°=60°.
Половина меньшей диагонали противолежит углу 30° и равна АВ:2=5 см
Вся диагональ ВВ₁=5*2=10 см
Приложения:
Новые вопросы
Математика,
2 года назад
Обществознание,
9 лет назад
Математика,
9 лет назад
Информатика,
9 лет назад