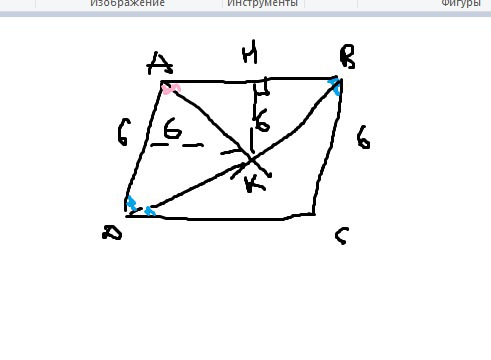
биссектрисы углов А и В параллелограма ABCD пересекаются в точке К. найдите площадь параллелограма, если ВС равен 6, а расстояние от точки К до тороны АВ равно 6
Ответы на вопрос
Ответил ЭхБылоВремя
0
Обозначим точки пересечения биссектрис со сторонами F и Е тогда
∠FAK=∠BEK (т.к. это накрест-лежащие углы).
Получается, что ∠BAK=∠BEK, следовательно треугольник ABE -равнобедренный (по свойству равнобедренного треугольника).
Тогда AB=BE.
Треугольники ABK и EBK равны по первому признаку равенства треугольников.
Следовательно и высоты у этих треугольников тоже равны.
Аналогично, равны и треугольники ABK и AFK.
Получается, что высота параллелограмма равна 2h.
Площадь параллелограмма равна S=2h*BC=2*6*6=72
Ответ: S=72
∠FAK=∠BEK (т.к. это накрест-лежащие углы).
Получается, что ∠BAK=∠BEK, следовательно треугольник ABE -равнобедренный (по свойству равнобедренного треугольника).
Тогда AB=BE.
Треугольники ABK и EBK равны по первому признаку равенства треугольников.
Следовательно и высоты у этих треугольников тоже равны.
Аналогично, равны и треугольники ABK и AFK.
Получается, что высота параллелограмма равна 2h.
Площадь параллелограмма равна S=2h*BC=2*6*6=72
Ответ: S=72
Ответил вика2485
0
ответ должен быть 72
Ответил gavryushа
0
Высота пар-ма будет равна =6*2 = 12(те. 2 высоты треугольника) и по формуле площади пар-ма S=ah=12*6=72
Приложения:
Ответил gavryushа
0
Понятно?
Ответил gavryushа
0
т.е. 4 треугольника умещаются в пар-ме
Ответил вика2485
0
теперь поняла!
Новые вопросы