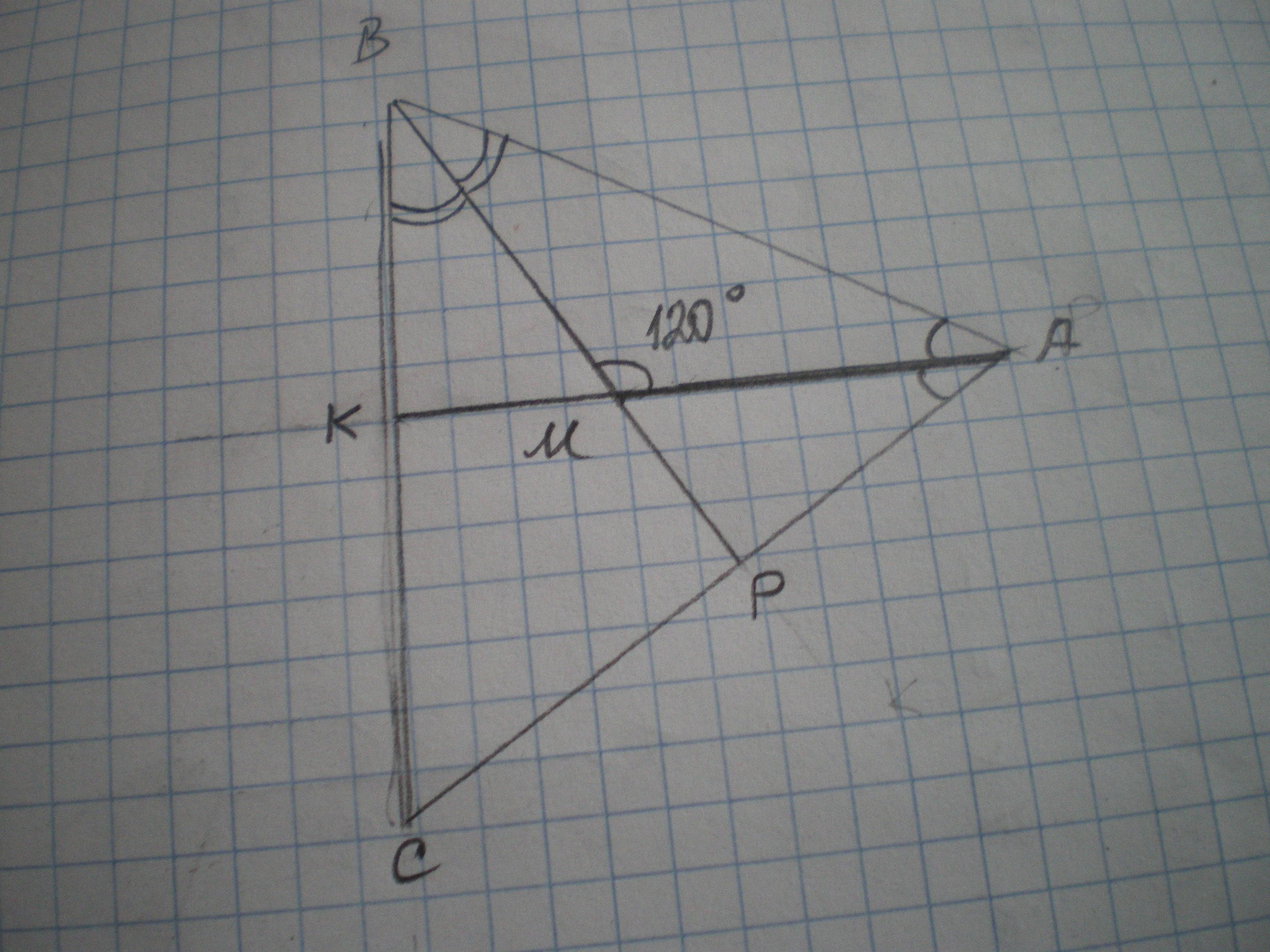
Биссектрисы углов A и B треугольника ABC пересекаются в точке M.
Найдите
∠A+∠B, если ∠AMB = 120
помогите

Ответ:

120°

Объяснение:

Дано: ΔАВС; ВР и АК - биссектрисы, ∠АМВ=120°. Найти ∠A+∠B.

∠МВА+∠МАВ=180-120=60°

∠А=2∠МАВ;  ∠В=2∠МВА по определению биссектрисы

∠А+∠В=60*2=120°