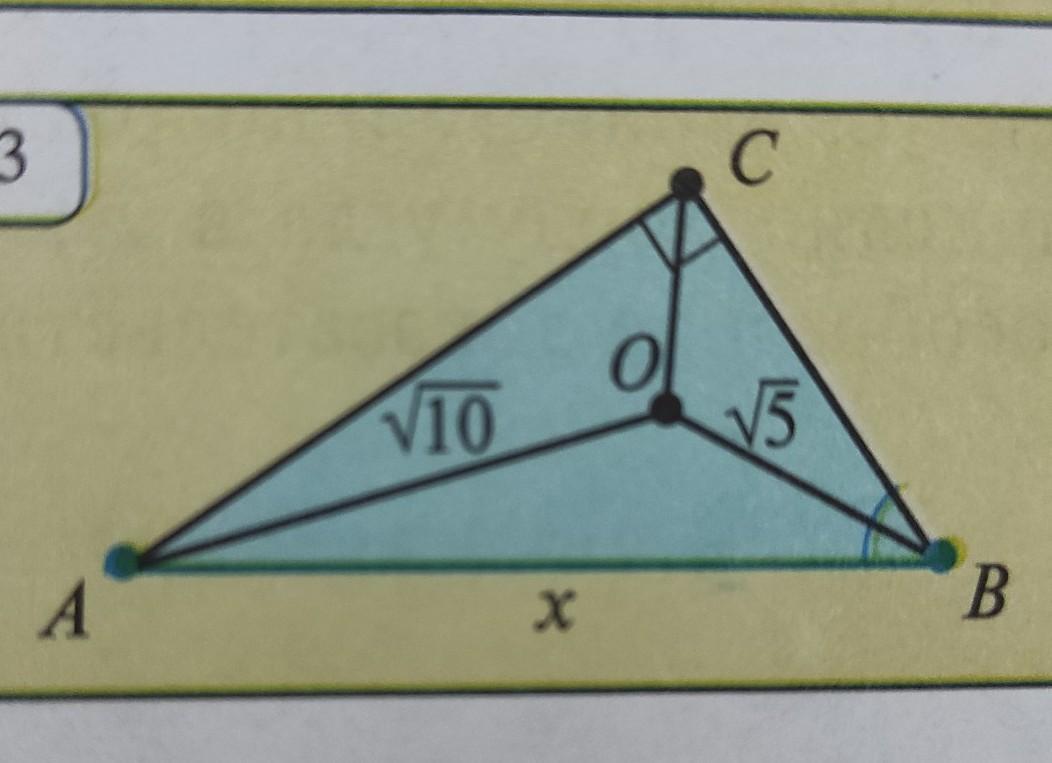
биссектрисы прямоугольного к ABC (C=90°) пересекаются в точке О . найдите гипотенузу , если AO =√10, OB =√5​

Рассмотрим треугольник ACB, ∠A + ∠B = 180°-90° = 90°

Рассмотрим треугольник AOB, ∠OAB + ∠OBA = 1/2∠A + 1/2∠B =

= 1/2(∠A + ∠B) = 1/2 * 90° = 45°

∠AOB = 180° - ∠OAB - ∠OBA = 180° - (∠OAB + ∠OBA) = 180° - 35° = 135°

По теореме косинусов :

x^2 = √10^2 + √5^2 - 2√5√10cos(135°)

x^2 = 10 + 5 - 2√50 * (-√2/2)

x^2 = 15 + √100

x^2 = 15+10

x^2 = 25

x = 5

Ответ : 5