биссектриса углов а и б треугольника абц пересекаются в точке м найди угол амб если угол abc равен 40 в угол асб равен 80
Приложения:
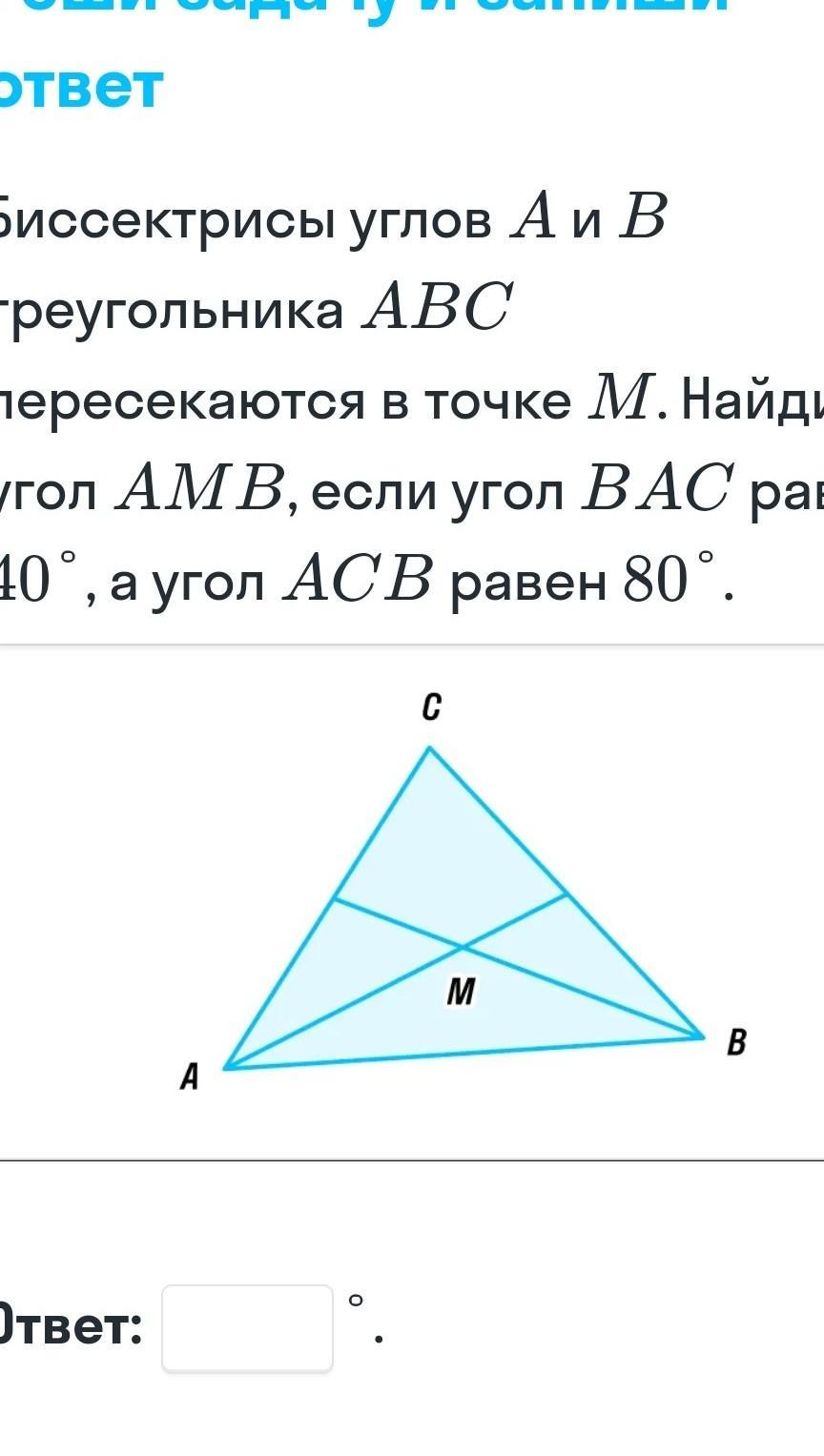
Ответы на вопрос
Ответил ReMiDa
0
Ответ:
130°
Объяснение:
Т.К. сумма углов треугольника равна 180°, то
∠САВ=180°-∠АВС-∠АСВ= 180°- 40° - 80° = 60°
Биссектрисой треугольника называется отрезок, который соединяет вершину с противоположной стороной и делит соответствующий угол пополам.
АМ - биссектриса ∠САВ ⇒ ∠МАВ=∠САМ=60°:2=30°
ВМ - биссектриса ∠АВС ⇒ ∠АВМ=∠СВМ=40°:2=20°
ΔАМВ: ∠АМВ = 180°- ∠МАВ - ∠АВМ = 180° - 30° - 20° = 130°
daniilborsik:
Demida помоги мне пожалуйста
Новые вопросы
Физика,
1 год назад
Химия,
1 год назад
Английский язык,
6 лет назад
История,
6 лет назад
Математика,
8 лет назад