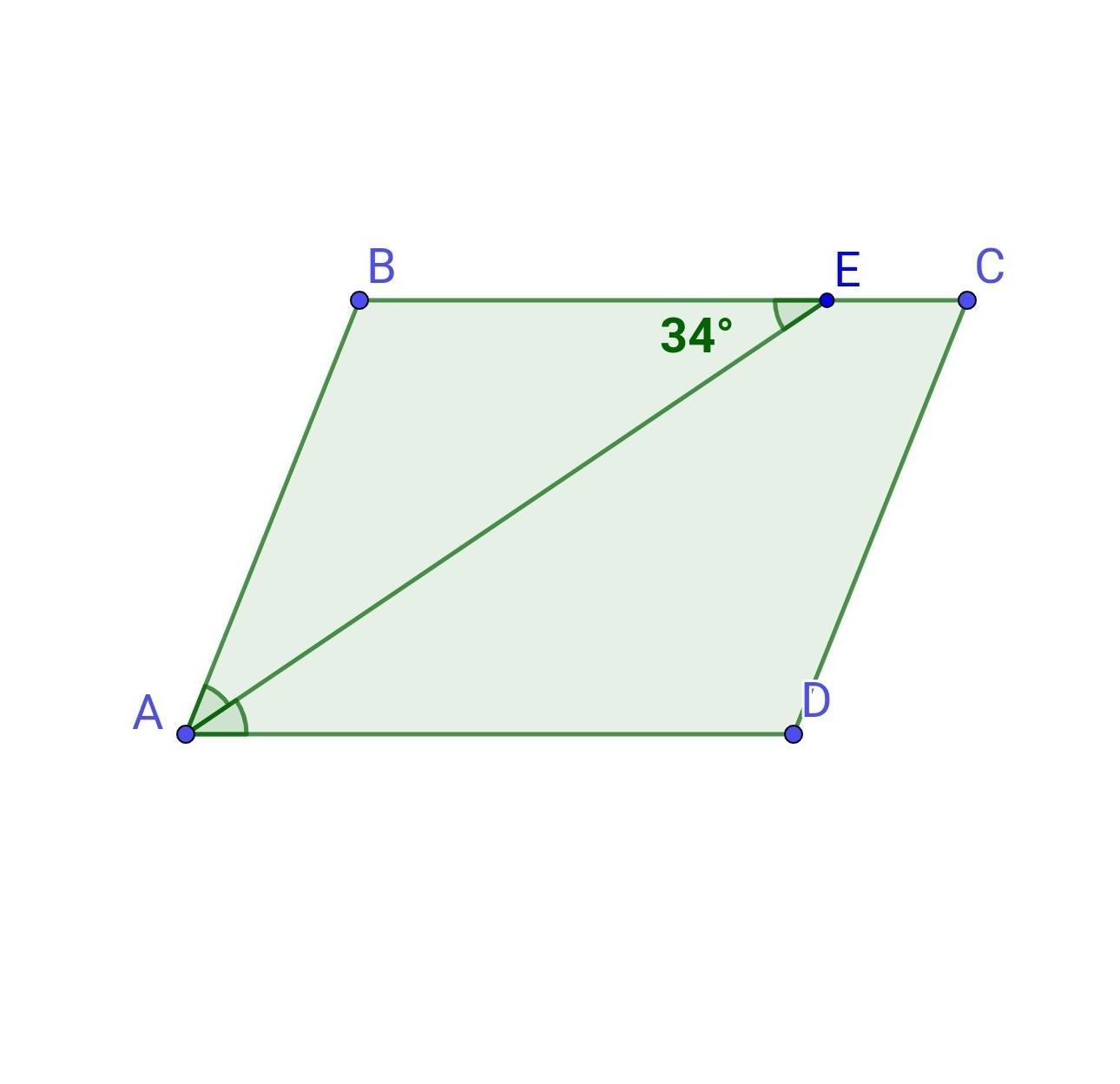
Биссектриса угла параллелограмма НЕ ПРОХОДИТ через точку пересечения диагоналей параллелограмма и пересекает его сторону, образуя с ней угол
34°. Найдите все углы параллелограмма.

Ответ:

Углы параллелограмма равны: 68°, 112°, 68°, 112°.

Объяснение:

Биссектриса угла параллелограмма НЕ ПРОХОДИТ через точку пересечения диагоналей параллелограмма и пересекает его сторону, образуя с ней угол 34°. Найдите все углы параллелограмма.

Дано: ABCD - параллелограмм. АЕ - биссектриса угла А. АЕ∩ВС=Е, ∠АЕВ=34°

Найти: ∠A, ∠B, ∠C, ∠D

Решение

1) ∠АЕВ=∠EAD - как внутренние накрест лежащие углы, образованные при пересечении параллельных прямых BC и AD и секущей АЕ.

Следовательно: ∠EAD=∠AEB=34°.

2) ∠BAE=∠EAD - по условию (АЕ - биссектриса).

Тогда ∠А=2•∠EAD=2•34°=68°.

3) ∠А+∠В=180° - как соседние углы параллелограмма. Тогда:

∠В=180°-∠А=180°-68°=112°.

4)∠C=∠A=68° - как противоположные углы параллелограмма.

5)∠D=∠B=112° - как противоположные углы параллелограмма.

Ответ: 68°,112°,68°,112°

#SPJ1