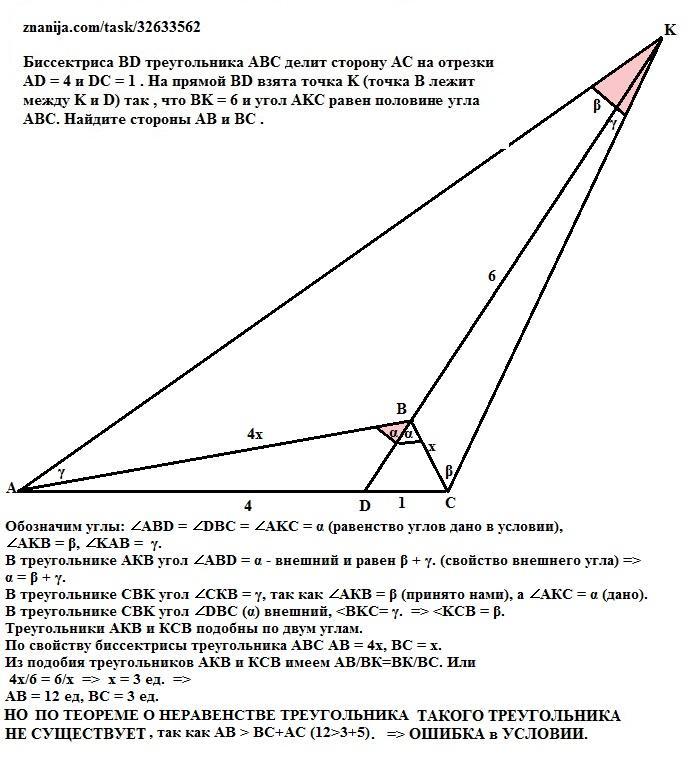
Биссектриса BD треугольника ABC делит сторону AC на отрезки AD = 4 и DC = 1 . На прямой BD взята точка K (точка B лежит между K и D) так , что BK = 6 и угол AKC равен половину угла ABC. Найдите стороны AB и BC .
2 < BK < 3,4
Ответы на вопрос
Ответ:
Треугольника АВС со сторонами АВ=12, ВС=3 и АС=5 НЕ СУЩЕСТВУЕТ.
Объяснение:
Обозначим углы: ∠ABD = ∠DBC = ∠AKC = α (равенство углов дано в условии),
∠AKB = β, ∠KAB = γ.
В треугольнике АКВ угол ∠ABD = α - внешний и равен β + γ. (свойство внешнего угла) => α = β + γ.
В треугольнике CBK угол ∠СКВ = γ, так как ∠АКВ = β (принято нами), а ∠АКС = α (дано).
В треугольнике CBK угол ∠DBC (α) внешний, <BKC= γ. => <KCB = β.
Треугольники АКВ и КСВ подобны по двум углам.
По свойству биссектрисы треугольника АВС АВ = 4х, ВС = х.
Из подобия треугольников АКВ и КСВ имеем
АВ/ВК=ВК/ВС. Или 4х/6 = 6/х => х = 3 ед. =>
АВ = 12 ед, ВС = 3 ед.
НО ПО ТЕОРЕМЕ О НЕРАВЕНСТВЕ ТРЕУГОЛЬНИКА ТАКОГО ТРЕУГОЛЬНИКА НЕ СУЩЕСТВУЕТ, так как
АВ > ВC+AC (12 > 3+5). => ОШИБКА в УСЛОВИИ.