Бисектриса угла делит его пополам,чему равны стороны параллелограмма если его периметр равен 30см?

Ответ:

В условиет нет достаточных данных. Проверь плиз

Если предположить что биссектриса делит противолежащую сторону попалам, то решение такое.

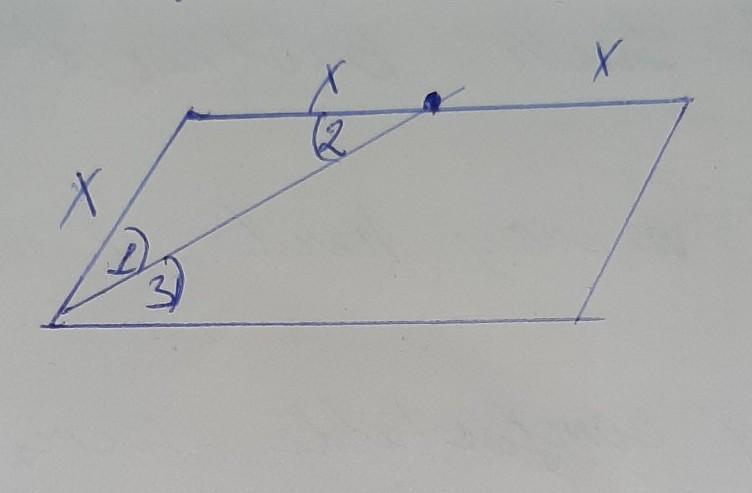
Треугольник образованный биссектрисой будет равнобедренным,

т.к углы 2 и 3 равны как внутренние накрест лежащие, а углы 1 и 2 равны потому что это биссектриса. Следовательно угол 1=углу 2

30÷2=15 сумма двух сторон

3Х=15

Х=5

Меньшая сторона 5, большая 10

Ответ:

Давайте обозначим стороны параллелограмма как a и b. Поскольку бисектриса угла делит его пополам, можно сказать, что каждая из сторон, образующих угол, делится пополам. Таким образом, длины сторон параллелограмма можно представить как a/2 и b/2.

Также известно, что периметр параллелограмма равен 30 см:

2a + 2b = 30

Теперь подставим выражения для сторон через a и b:

2 × а/2 + 2 × b/2 = 30

Упростим уравнение:

a + b = 15

Таким образом, сумма длин сторон параллелограмма равна 15 см. Однако это уравнение не дает нам однозначного решения для a и b. Например, стороны могут быть равны 7.5 см и 7.5 см, или 8 см и 7 см, и так далее. Такие пары сторон удовлетворяют условиям задачи.