Бічне ребро прямої чотирикутної призми дорівнює 5 см. Знайдіть площу
повної поверхні призми, якщо її основа – прямокутник, діагональ якого дорівнює
10 см, а одна зі сторін – 8 см.

Ответ:

Площа повної поверхні призми дорівнює 236 см²

Объяснение:

Бічне ребро прямої чотирикутної призми дорівнює 5 см. Знайдіть площу повної поверхні призми, якщо її основа – прямокутник, діагональ якого дорівнює 10 см, а одна зі сторін – 8 см.

• Пряма призма - призма, бічні ребра якої перпендикулярні до площин основи.
• Площа повної поверхні призми обчислюється за формулою:

Sп = Sб + 2Sосн.

де Sб = Pосн • H (H - висота призми) - площа бічної поверхні

Sосн - площа основи.

Так як призма пряма, то її бічне ребро є висотою призми.

Розв'язання

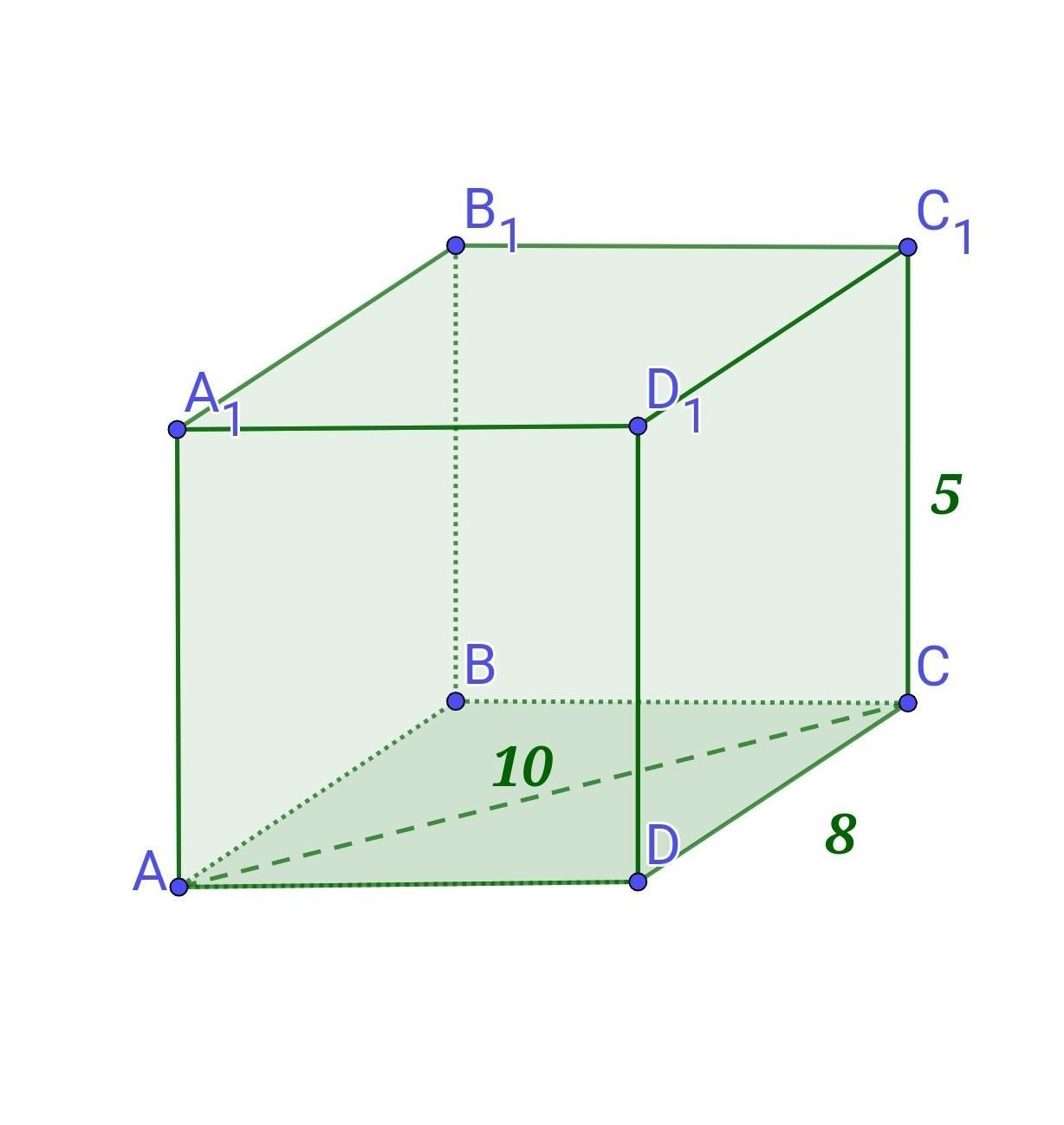
Нехай ABCDA₁B₁C₁D₁ - дана чотирикутна призма. Висота СС₁=5 см, АС = 10 см, DC = 8 см

Знайдемо Sп.

1.

Так як в основі призми лежить прямокутник, то △ACD - прямокутний, ∠D=90°.

За теоремою Піфагора знайдемо катет AD:

AD²= AC²-DC²

AD²=10²-8²=100-64=36

AD = 6 (см)

2.

Знайдемо бічну поверхню призми.

Pосн = 2(AD+DC) = 2(6+8) = 2 • 14 = 28 (см)

Sб = 28 • 5 = 140 (см²)

3.

Знайдемо площу основи призми (прямокутника ABCD):

Sосн = S(ABCD) = AD • DC = 6 • 8 = 48 (см²)

4.

Sп. = 140 + 2 • 48 = 140 + 96 = 236 (см²)

#SPJ1