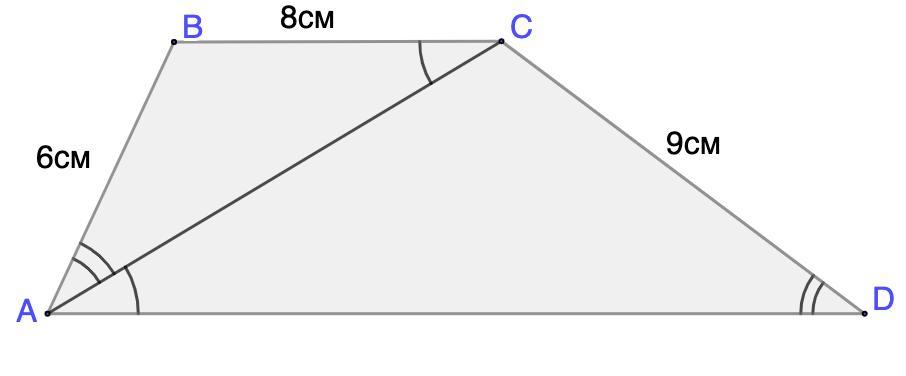
Бічні сторони трапеції дорівнюють 6 см і 9 см, а менша основа 8 см. Знайдіть довжину більшої основи, якщо діаго­наль ділить трапецію на два подібні трикутники.

Ответ:

Длина большего основания трапеции равна 18 см.

Пошаговое объяснение:

Боковые стороны трапеции равны 6 см и 9 см, а меньшее основание 8 см. Найдите длину большего основания, если диагональ делит трапецию на два подобных треугольника.

Дано: ABCD - трапеция,

АВ = 6 см; CD = 9 см; ВС = 8 см;

ΔABC ~ ΔACD.

Найти: AD

Решение:

Рассмотрим ΔABC и ΔACD.

ΔABC ~ ΔACD (по условию)

Определимся с равными углами.

∠ВСА = ∠САD (накрест лежащие при ВС || AD и секущей АС)

Тогда два других острых угла тоже равны.

⇒ ∠ВАС = ∠СDA

А также равны углы:

∠АВС = ∠ACD.

• В подобных треугольниках против равных углов лежат сходственные стороны.

Запишем отношения сходственных сторон:

Сначала найдем АС:

 (см)

Теперь найдем AD:

 (см)

Длина большего основания трапеции равна 18 см.

#SPJ1