ax2+y2-6x+5=0
поможіть бистро
Ответы на вопрос
Ответ:
Решение:
a) Уравнение окружности:
(х - х0)² + (y - y0)² = r², где
(х0, у0) - координаты центра
r - радиус
Приведем наше уравнение к такому виду с помощью выделения полных квадратов:
х² + y² - 6x - 4y + 5 = 0
(x² - 6x) + (y² - 4y) + 5 = 0
(x² - 2*3*x) + (y² - 2*2*y) + 5 = 0
(x² - 2*3*x + 3² - 3²) + (y² - 2*2*y + 2² - 2²) + 5 = 0
(x² - 2*3*x + 3²) - 3² + (y² - 2*2*y + 2²) - 2² + 5 = 0
(x - 3)² - 9 + (y - 2)² - 4 + 5 = 0
(x - 3)² + (y - 2)² = 9 + 4 - 5
(x - 3)² + (y - 2)² = 8
Итого:
Центр: (3, 2)
Радиус: \sqrt{8}
8
b) В точках, где окружность пересекается с Ох, у = 0. Найдем эти точки:
(х - 3)² + (y - 2)² = 8
(х - 3)² + (0 - 2)² = 8
(х - 3)^2 + (-2)² = 8
(х - 3)² + 4 = 8
(х - 3)² = 8 - 4
(х - 3)² = 4
x - 3 = 2 или х - 3 = -2
x = 5 или х = 1
Итого:
А: (1, 0)
В: (5, 0)
с) Найти площадь можно двумя способами.
Способ I: Занудный
Формула Герона:
S = \sqrt{p*(p - a)*(p - b)*(p - c)}
p∗(p−a)∗(p−b)∗(p−c)
, где
a, b, c - стороны треугольника
р - полупериметр
Обозначим центр точкой О.
Имеем:
О (3, 2)
А (1, 0)
В (5, 0)
ОА и ОВ - радиусы, равные \sqrt{8}
8
AB = 5 - 1 = 4
=> p = (4 + \sqrt{8}
8
+ \sqrt{8}
8
) / 2 = 2 + \sqrt{8}
8
S = \sqrt{(2 + \sqrt{8} ) * (2 +\sqrt{8} -\sqrt{8} ) * (2 + \sqrt{8} - \sqrt{8} ) * (2 + \sqrt{8} - 4)}
(2+
8
)∗(2+
8
−
8
)∗(2+
8
−
8
)∗(2+
8
−4)
=
\sqrt{(2+\sqrt{8} ) * 2 * 2 * (\sqrt{8} - 2) }
(2+
8
)∗2∗2∗(
8
−2)
=
\sqrt{(8 - 4) * 2 * 2}
(8−4)∗2∗2
= 4
Способ II: Быстрый
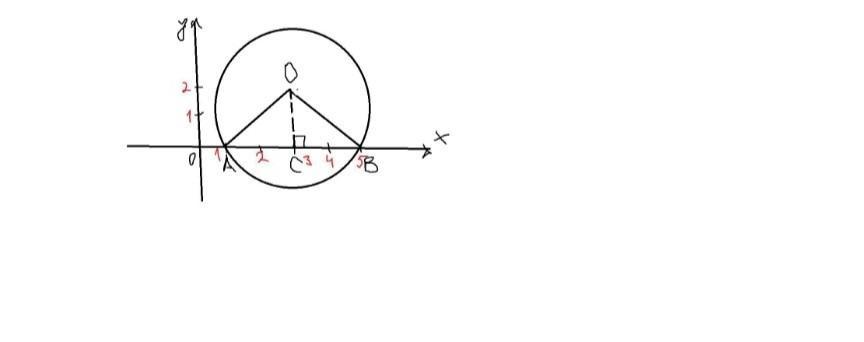
Сделаем дополнительное построение: опустим перпендикуляр из центра на Ох. Так как центр находится в точке (3, 2), перпендикуляр попадет в точку (3, 0). Пусть это будет точка С.
Имеем:
О (3, 2)
А (1, 0)
В (5, 0)
С (3, 0)
Найдем АС и ВС:
АС = 3 - 1 = 2
ВС = 5 - 3 = 2
Рассмотрим треугольники АОС и ВОС:
ОА = ОВ (как радиусы)
ОС - общая сторона
АС = ВС = 2
=> равны по трем сторонам.
Найдем площадь одного из них.
ОАС прямоугольный (по построению ОС), поэтому его площадь находится по формуле:
S = a*b / 2, где
a, b - катеты
OC = 2 - 0 = 2
AO = 2,
поэтому S = 2*2/2 = 2
Треугольники одинаковы, поэтому площадь ОСВ тоже 2.
Следовательно, их общая площадь равна 2 + 2 = 4.