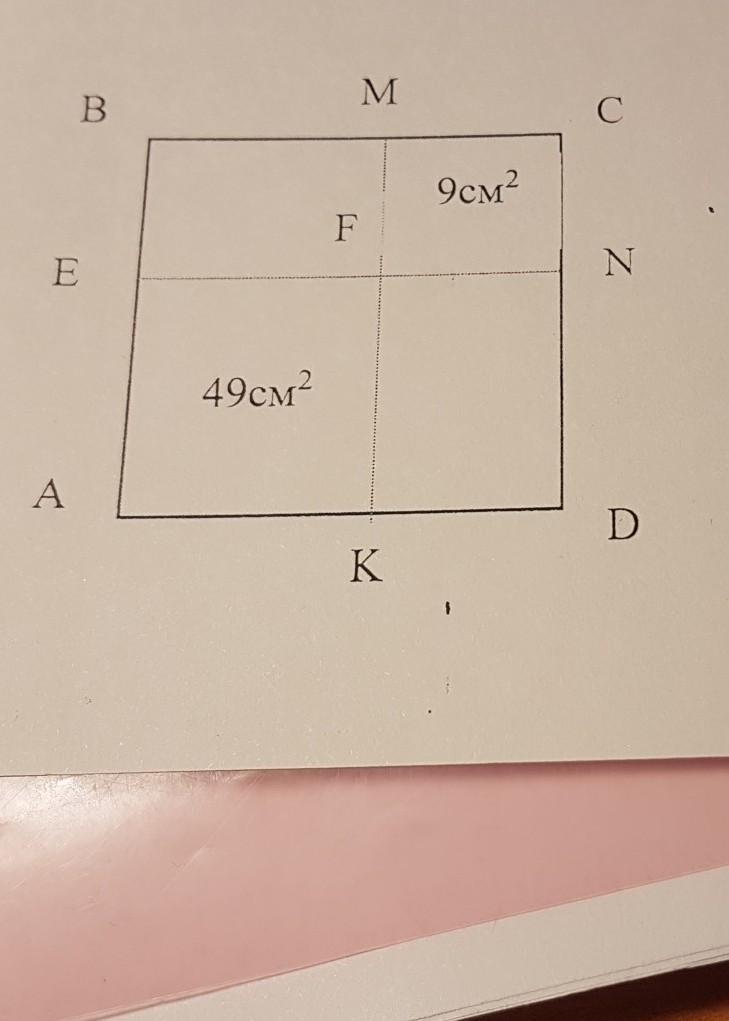
АВСD квадрат. AEFK квадрат.FMCN квадрат .найти площать ABCD.срочно
Ответы на вопрос
Ответ:
100 см^2
Пошаговое объяснение:
Сначала находим стороны AE = AK и MC = CN.
AE = AK = sqrt(S(AEFK)) = sqrt(49) = 7см.
MC = CN = sqrt(S(FMCN)) = sqrt(9) = 3см.
Поскольку эти квадраты касаются друг друга в точки F, то можем заключить, что KD = MC, значит AD = AK + MC = 7+3 = 10.
S(ABCD) = AD^2 = 10^2 = 100см^2.
Так как AEFK квадрат, то его стороны равны по 7 см. FMCN тоже квадрат, следовательно стороны равны 3 см. Тогда KFND- прямоугольник со сторонами 7 и 3 см и его площадь равна 7*3=21 см^2.
EBMF также прямоугольник со сторонами 7 и 3 см, его площадь 21 см^2. Площадь самого квадрата ABCD равна сумме площадей фигур внутри, то есть 21+21+9+49=100 см^2.
Другой способ. Так как AEFK квадрат, то KF=ND=7 см. Так как FMCN квадрат, то FM=EB=3 см. Тогда AB=AE+EB=7+3=10 см. В квадрате все стороны равны, следовательно все стороны по 10 см, тогда площадь 10*10=100 см^2