Алгебра, тригонометрия! 80 баллов, объясните подробно каждый шаг, пожалуйста. Подробности на фото ниже:
Приложения:
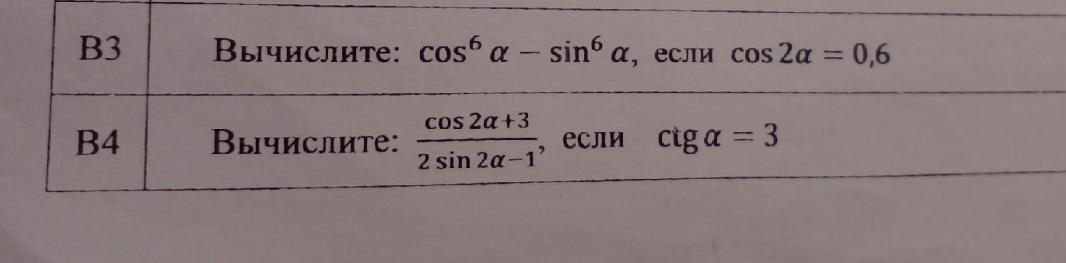
Ответы на вопрос
Ответил hote
1
B3
Дано
упростим выражение
B4
Дано:
Упростим выражение
заменим cosa=3sina
krispootomato:
Спасибо!
Новые вопросы
Русский язык,
1 год назад
Английский язык,
1 год назад
Английский язык,
6 лет назад
Алгебра,
6 лет назад
Геометрия,
8 лет назад