Алгебра, вопрос задал lawskija , 2 года назад

Алгебра ПОВИННО БУТИ!! 1.ЗВЕДЕННЯ ДО СПІЛЬНОГО ЗНАМЕННИКА
2.ЗНАХОДЖЕННЯ ОДЗ
3.РОЗВ'ЯЗУВАННЯ КВАДРАТНОГО рівняння з повним розписуванням

Приложения:

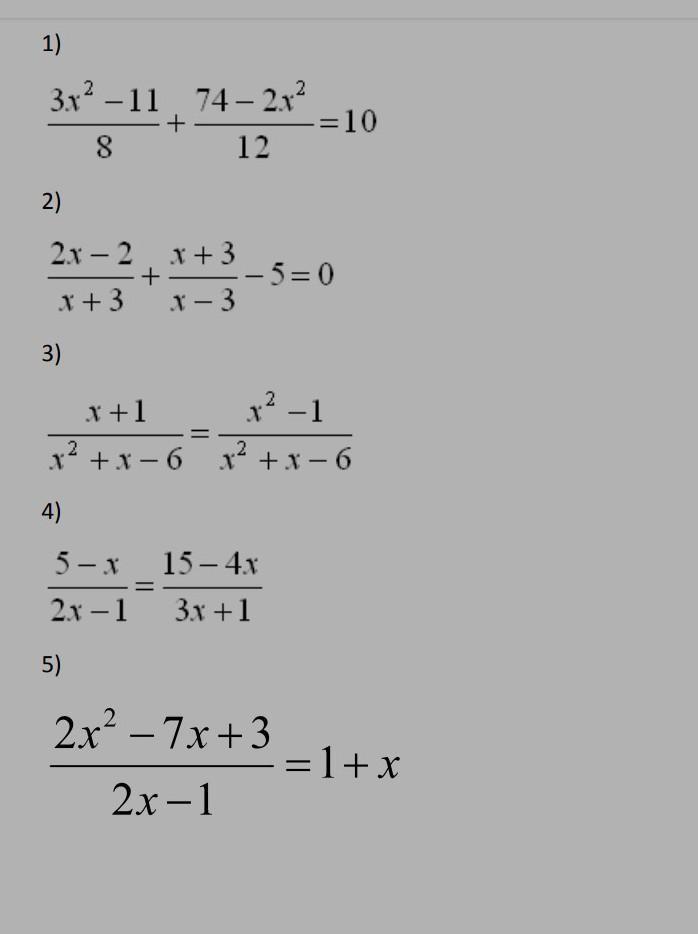
Ответы на вопрос

Ответил MuhammadGulu

$1)$

$\frac{3 {x}^{2} - 11 }{8} + \frac{74 - {2x}^{2} }{12} = 10 \\ \frac{ {9x}^{2} - 33 + 148 - {4x}^{2} }{24} = 10 \\ {5x}^{2} + 115 = 10 \\ {5x}^{2} = - 105 \\ {x}^{2} = - 21 \\ x = ∅$

Т.к в квадрате никогда не может быть отрицательное число значит уравнение не имеет значения

$2)$

$\frac{2x - 2}{x + 3} + \frac{x + 3}{x - 3} - 5 = 0 \\ \frac{(2x + 2)(x - 3) + (x + 3)(x + 3)}{(x - 3)(x + 3)} - 5 = 0 \\ \frac{ {2x}^{2} - 6x + 2x - 6 + {x}^{2} + 3x + 3x + 9 }{ {x}^{2} - 9} - 5 = 0 \\ \frac{ {3x}^{2} + 2x + 3 }{ {x}^{2} - 9} - 5 = 0 \\ \frac{ {3x}^{2} + 2x + 3 - 5 {x}^{2} + 45}{ {x}^{2} - 9} = 0 \\ - {2x}^{2} + 2x + 48 = 0 \\ {x}^{2} - x - 24 = 0$

$D = {( - 1)}^{2} - 4 \times 1 \times ( - 24) = 1 + 24 = 25$

$x1x2 = \frac{ - ( - 1)± \sqrt{25} }{2 \times 1} = \frac{1±5}{2} = - 2 \:; \: 3\\$

Формула Дискриминанта:

$D = {b}^{2} - 4ac$

Формула x1x2:

$x1x2 = \frac{ - b± \sqrt{D} }{2a} \\$

Где:

D - Дискриминант

а - число перед х²

b - число перед х

c - число без х

$3)$

$\frac{x + 1}{ {x}^{2} + x - 6} = \frac{ {x}^{2} - 1 }{ {x}^{2} + x - 6 } \\$

x² + x -6 cокращается.

$x + 1 = {x}^{2} - 1 \\ {x}^{2} - 1 - x - 1 = 0 \\ {x}^{2} - x - 2 = 0 \\ x1 + x2 = 1 \\ x1 \times x2 = - 2 \\ x1 = 2 \: \: \: \: \: x2 = - 1$

Теорема Виета:

х1 + х2 = -p

x1 • x2 = q

Где:

p - число перед х

q - число без х

$4)$

$\frac{5 - x}{2x - 1} = \frac{15 - 4x}{3x + 1} \\ (5 - x)(3x + 1) = (15 - 4x)(2x - 1) \\ 15x + 5 - {3x}^{2} - x = 30x - 15 - {8x}^{2} + 4x \\ - 3 {x}^{2} + 14x + 5 + {8x}^{2} - 34x - 15 = 0 \\ 5 {x}^{2} - 20x - 10 = 0 \\ {x}^{2} - 4x - 2 = 0$

$D = {( - 4)}^{2} - 4 \times 1 \times ( - 2) = 16 + 8 = 24$

$x1x2 = \frac{ - ( - 4)± \sqrt{24} }{2 \times 1} = \frac{4± \sqrt{24} }{2} \\$

$x1x2 = \frac{4 + \sqrt{24} }{2} \: ; \: \frac{4 - \sqrt{24} }{2} \\$

$5)$

$\frac{2 {x}^{2} - 7x + 3 }{2x - 1} = 1 + x \\ {2x}^{2} - 7x + 3 = (1 + x)(2x - 1) \\ {2x}^{2} - 7x + 3 = 2x - 1 + {2x}^{2} - x \\ {2x}^{2} - 7x + 3 - 2x + 1 - {2x}^{2} + x = 0 \\ - 8x + 4 = 0 \\ - 8x = - 4 \\ x = 0.5$