Алгебра помогите 3 примера, я неспешу просто сделайте пж
Приложения:


natalyabryukhova:
проверьте 2 пример
Ответы на вопрос
Ответил natalyabryukhova
1
Объяснение:
Использовали формулы сокращенного умножения:
Приложения:
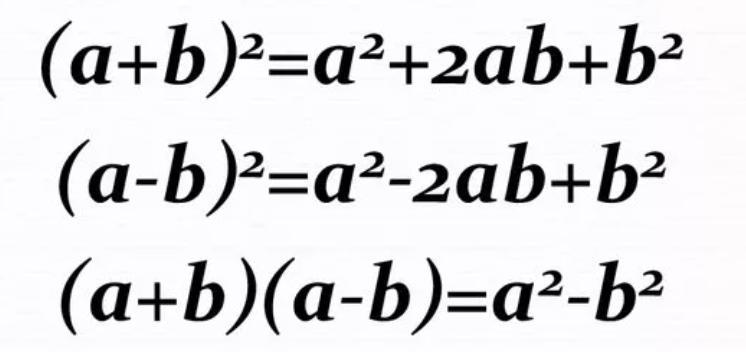
Новые вопросы
Русский язык,
1 год назад
Русский язык,
1 год назад
География,
6 лет назад
Математика,
6 лет назад
Алгебра,
8 лет назад