Алгебра, вопрос задал Лилио , 2 года назад

Алгебра. Логарифмы. Помогите!

Приложения:

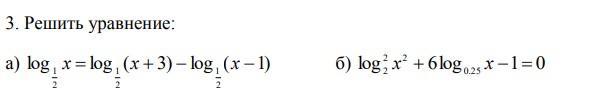
Ответы на вопрос

Ответил hote

$\displaystyle log_{1/2}x=log_{1/2}(x+3)-log_{1/2}(x-1)\\\\ODZ:\left \{ {{x>0; x+3>0} \atop {x-1>0}} \right.; x>1\\\\log_{1/2}x+log_{1/2}(x-1)=log_{1/2}(x+3)\\\\log_{1/2}(x^2-x)=log_{1/2}(x+3)\\\\x^2-x=x+3\\\\x^2-2x-3=0\\\\D=4+12=16\\\\x_1=3; x_2=-1$

но х>0 значит корень только х=3

б)

$\displaystyle log^2_2x^2+6log_{0.25}x-1=0\\\\ODZ:x>0\\\\(2log_2x)^2+6log_{\frac{1}{4}}x-1=0\\\\4log^2_2x+6*log_{2^{-2}}x-1=0\\\\4log^2_2x-3log_2x-1=0\\\\log_2x=t\\\\4t^2-3t-1=0\\\\D=9+16=25\\\\t_1=1; t_2=-\frac{1}{4}\\\\log_2x=1; x=2\\\\log_2x=-\frac{1}{4}; x=2^{-\frac{1}{4}}; x=\frac{1}{\sqrt[4]{2}}$

оба корня подходят под ОДЗ

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

Найти подлежащее в тексте .Медленно падали большие и красивые снежинки . Подлежащее - большие и красивые снежинки ? Или только снежинки...

Русский язык, 1 год назад

Есть ли в русском языке разные слова обозначающие одно и то же слово?

История, 2 года назад

защёт чего америка начала развиваться в 19 веке...

Русский язык, 2 года назад

Помошите страница 5 плз...

Математика, 8 лет назад

1376:172 Сделать прикидку Плиз...

История, 8 лет назад

Наука, которая изучает историю письма это:...