Алгебра, вопрос задал Мозгокошка , 1 год назад

Алгебра даю 100 баллов за лучший ответ!Всего 2 задания

Приложения:

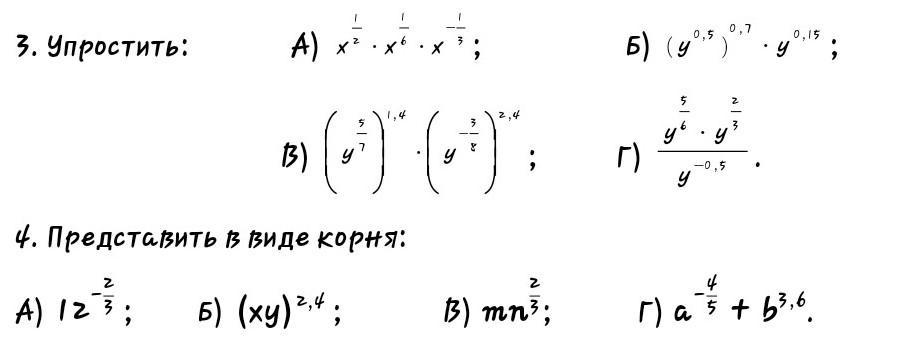
Ответы на вопрос

Ответил NNNLLL54

3

Ответ:

Применяем свойства степеней:

$\bf a^{n}\cdot a^{m}=a^{n+m}\ \ ,\ \ (a^{n})^{m}=a^{n\cdot m}\ \ ,\ \ a^{n}:a^{m}=a^{n-m}$

$1)\ \ x^{\frac{1}{2}}\cdot x^{\frac{1}{6}}\cdot x^{\frac{1}{3}}=x^{\frac{1}{2}+\frac{1}{6}+\frac{1}{3}}=x^{\frac{6}{6}}=x\\\\(y^{0,5})^{0,7}\cdot y^{0,15}=y^{0,35}\cdot y^{0,15}=y^{0,5}=\sqrt{y}\\\\\Big(y^{\frac{5}{7}}\Big)^{1,4}\cdot \Big(y^{-\frac{3}{8}}\Big)^{2,4}=y^1\cdot y^{-0,9}=y^{1-0,9}=y^{0,1}\\\\\dfrac{y^{\frac{5}{6}}\cdot y^{\frac{2}{3}}}{y^{-0,5}}=\dfrac{y^{\frac{9}{6}}}{y^{-0,5}}=y^{\frac{3}{2}+0,5}=y^2$

2) Представить в виде корня:

$a)\ \ 12^{-\frac{2}{3}}=\sqrt[3]{12^{-2}}=\sqrt[3]{-144}\\\\(xy)^{2,4}=(xy)^{\frac{12}{5}}=\sqrt[5]{(xy)^{12}}=\sqrt[5]{x^{12}\, y^{12}}\\\\m\, n^{\frac{2}{3}}=m\, \sqrt[3]{n^2}=\sqrt[3]{m^3\, n^2}\\\\a^{-\frac{4}{5}}+b^{3,6}=\sqrt[5]{a^{-4}}+b^{\frac{18}{5}}=\sqrt[5]{a^{-4}}+\sqrt[5]{b^{18}}=\dfrac{1}{\sqrt[5]{a^{4}}}+\sqrt[5]{b^{18}}$

Мозгокошка: вы просто золото.Огромное вам спасибо за помощь

saman110: Извините можете просмотреть и мое задание по математике

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

помогите один омоним слова четыре синоним слова помогите пожалуста...

Русский язык, 1 год назад

Помогите...дам 50 баллов!!! Согласно Закону "Об образовании в РФ"ученики обязаны добросовестно осваивать образовательную программу,выполнять индивидуальный учебный план,посещать предусмотренные...

Химия, 1 год назад

Укажіть електронні аналоги Кальцію: а)K б)Mq в)Sr г)Al...

Математика, 1 год назад

запиши всі двоцифрові числа у яких цифра розряду одиниць на 3 менша за цифру розряду десятків .допоможіть...

Математика, 7 лет назад

ПРОШУ ПОМОЧЬ. МНЕ ОЧЕНЬ НУЖНО. БУДЬТЕ ЛЮБЕЗНЫ. МНЕ ОЧЕНЬ НЕОБХОДИМО.

Математика, 7 лет назад

В лагерьЗубренок прибыло 240 учеников из Минска и Орши. мальчиков среди прибывших было 125 человек,из которых 65 минчане.в числе учеников прибывших из Орши, девочек было 53.сколько всего учеников...